18. Simulating Differential Equations
Section author: Malcolm Smith <msmith.malcolmsmith@gmail.com>
[status: first draft]
18.1. Motivation, Prerequisites, and Plan
Motivation
The world, at nearly every level, is described in differential equations. From Newton’s laws of motion on the planetary scale to the behavior of quantum particles, these equations are a fundemental part of the universe. In this chapter, the goal is to have a more concrete understanding of these equations and why they are so fundamentally useful, in addition to learning how to model them. If you are looking at the book as a whole, you may notice another chapter on differential equations. It is also a good chapter, and explains differential equations well. However, we will be using another approach to them. First, we will be solving them iteratively, rather than analytically. Second, we will study systems rather than individual equations. If you don’t know what that means, don’t worry, the next section will explain it in detail.
Prerequisites
The 10-hour “Serious Programming” course
The “Data files and first plots” mini-course in Section 2
The “Differential Equations” mini-course in Section 17
Plan
The plan for this mini-course is to first do a quick review of what differential equations are, and then outline the idea of a system of differential equations. From there, we will devise a simple set of differential equations to model salt concentrations in tanks of water. We will then discuss how this example can be connected to the more complex systems of differential equations, such as those governing planetary motion.
18.2. What is a Differential Equation?
To understand a differential equation, we must first understand the derivative. There are many ways to do this, though I will try to use the most intuitive version.
Imagine you are in a car, which is actively accelerating. The question is, after, say, 2 seconds of acceleration, how fast are you going? And for the purposes of this question, “after 2 second” refers to the precise moment in time, not any sort of small range. This seems like an impossible problem; at an given moment, nothing is moving (if this reminds you of Zeno’s paradox about the arrow, you’re in luck, because we will actually discuss the resolution to this particular “paradox” in the chapter).
However, what if we look from 1.9 to 2.1 seconds? Then, using the formula for speed you have undoubtedly used before, we can calculate speed. Speed = distance / time, though in this case speed would probably be more accurately defined as velocity. Regardless, this is easy to calculate: let us say you traveled 2 meters in those 0.2 seconds. In this case, speed = 2 meters / 0.2 seconds, or 10 meters per second. This is around 22 miles per hour, which seems pretty reasonable given the increasingly ridiculous 0 to 60s that have been appearing recently. We could be even more accurate than this, though. What if we measure from 1.99 seconds to 2.01 seconds? Already, we are getting to very small time intervals, which will give very good approximations of speed. In this case, the car went maybe 0.22 meters in the 0.02 seconds. This means the average speed over this interval was higher than the average speed over the longer interval, which could mean any number of things. Regardless, we have a refined estimate for speed: 11 m/s (around 25 mph). We can keep decreasing the time interval, and the speed over that interval should eventually converge to some value that we could say the car was going at precisely two seconds. This is the derivative, and it is one of two fundamental features of calculus.
Note that this is not the way you would see the derivative taught in a calculus class; rather, you would probably first be taught rigorous ways to take limits and then the graphical approach to derivatives. This second part is something we will also take a look at, though the first is unnecessary for an intuitive grasp of the derivative.
If you remember being taught how to calculate speed, chances are you had a graph of position vs. time at some point. You also probably remember finding the average speed by picking two points and finding the slope between them. This is what’s known as a secant line, and the slope is equivalent to the examples we had earlier about the speed of a car over shorter and shorter ranges. If we take this to the extreme, you can imagine allowing the two points to touch, and finding the slope at an exact point. This is the graphical understanding of the derivative, and is visualized below:
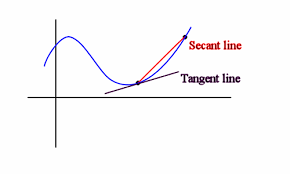
Figure 18.2.1 A simple graph illustrating the graphical interpretation of the derivative.
Keep in mind that learning the derivative in-depth is the subject of a college-level math class. Don’t feel bad if you find yourself confused by it at some points; just remember, it’s the rate of change at a specific point.
Now that we understand derivatives, let us look at differential equations. A differential equation is an equation that defines itself in terms of its derivative. This is a very odd concept, but it makes writing some equations much easier. For example, any exponential equation is easy to write like this. In the case of
it can be in a way that more directly shows its features:
In case you don’t know, one of the defining features of an exponential function is that the current growth rate is proportional to the current value. This helps to explain why the explode upward so dramatically, and can be seen in this example extremely clearly. The derivative (symbolized by \(f'(x)\)) is equal to some constant (\(ln(2)\)) times the current value of the function.
Another thing modeled by differential equations are the orbits of planets. This is because we can calculate the forces on an object at any given point in space, and thus the acceleration with \(F = ma\), but this doesn’t tell us the shape of the orbit. What is does give us is something called a second-order differential equation. What this means is that we can define the second derivative of the position in terms of the current position. What is a second derivative? It’s the derivative of the derivative, or how fast the derivative is changing. This is a tricky concept to grasp, which is why this is not a case we will be modeling. However, the reason why we get a second derivative in this case is clear: velocity is the rate of change of position, and acceleration (which we calculated from position) is the rate of change of velocity. When you solve these equations, they predict that planetary motion will follow an elliptical path. And indeed, that is exactly what is observed in nature, as shown in Figure 18.2.2:
Figure 18.2.2 A planet’s orbit around a star.
A final word before moving on to the programming: the notation for derivative we will be using for the rest of the chapter is not the one we have been using so far, because it is somewhat confusing learn in parallel with the concept of derivatives. \(\frac{df(x)}{dx}\), or \(\frac{df}{dx}\) for short, is the derivative of \(f(x)\) with respect to x. Earlier, in the car example, we were using time as the reference, so that was the derivative of the car’s position with respect to time. In this case, we are just taking the derivative with respect to the variable of the function. The graphical interpretation of this is the variable represented on the x-axis, and the thing you are taking the derivative of is on the y-axis. For all of the models in this chapter, everything will be relative to time, so this concept is not absolutely necessary to understand, but this is the notation we will be using.
18.3. Programming and Solving Differential Equations
To program a differential equation, we will avoid finding the precise, analytic solution to it and instead focus on iterating forward a small step in time. Effectively, this means keeping track of the current value of the function, the updating that based on our differential equation. Before we do that, though, we must discuss systems of differential equations.
Systems of differential equations are like regular systems of equations, only with differential equations instead. You use them when you are keeping track of more than one variable (as in the planet example above; we actually have two coordinates, x and y). In terms of programming, they work the exact same as the method we described above. For those without much math background, this may be a confusing topic, so let us discuss a simple example often used to teach this concept.
Imagine Romeo and Juliette’s love for each other can be modeled by differential equations (an odd concept, but bear with me). Specifically, the change in his love is equal to her love (\(dR/dt = J\)), and the change in her love is equal to the negative of his love (\(dJ/dt = -R\)). This is quite simple to program, as seen below:
from matplotlib import pyplot as plt
import numpy as np
def main():
r = 5
j = 5 ## initial conditions
rs = [r]
js = [j]
step_count = 750
step_size = 0.01
for _ in range(step_count):
r, j = iterate(r, j, step_size)
rs.append(r)
js.append(j)
plt.plot(np.arange(step_count + 1) * step_size, rs)
plt.plot(np.arange(step_count + 1) * step_size, js)
plt.show()
def iterate(r, j, step_size):
"""step r and j forward"""
r += step_size * j
j -= step_size * r
return r, j
There are a couple things to notice in this program. First of all, it is iterative, which means error can be cumulative and build up exponentially. Second, we are multiplying the derivatives by the step size. This is because the derivative in scaled to a step of 1 unit in the time direction, and we are stepping less than that, so the corresponding shift in love should be lower as well.
When run, this program should produce a pair of sinusoidal waves, as shown in Figure 18.3.1:
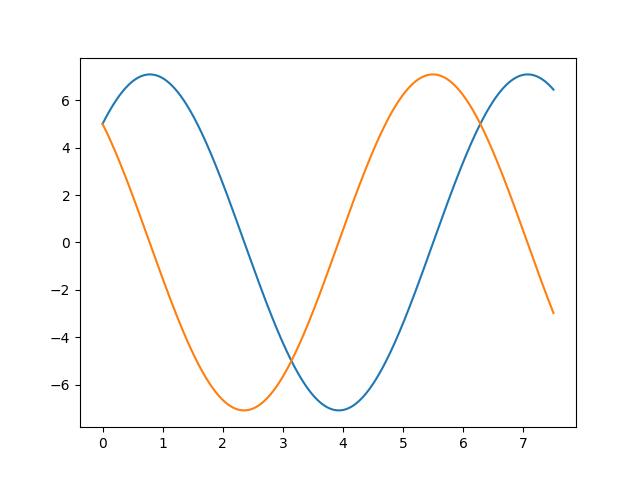
Figure 18.3.1 Romeo and Juliette’s love for each other over time.
There are several important implications of this simple model. First, complex behaviors (such as sine waves) can emerge from simple rules. This is an effect we will continue to see throughout the chapter, and is good to have in mind. The second is that a system of differential equations can have multiple solutions (known as families of solutions). In this case, we chose the starting point where both of them had a 5. However, we just as easily could have chosen any other pair of numbers, which would have resulted in a different set of waves.
Now that we have the basic structure for modeling these equations down, let us look at a more complex system to model. We will look at salt concentrations in tanks of water, which we can connect in various ways and with various flow rates. For the first example, we will have 3 tanks, each connected to one other:
Figure 18.3.2 Three tanks, with water flowing circularly.
In addition, as you may be able to tell by the diagram, tank A is twice the size of the other two. The importance of this will become apparent in a second. The other important necessity of this setup is that an equal amount of water is flowing in each pipe. After a moment of thought, this should be obvious: after all, if they weren’t equal, one tank would end up at more than capacity at some point which wouldn’t actually happen. To code this, we must first understand what’s happening to the salt concentration in a given tank at a given point in time. Take tank B, for example. If we assume the flow rate over a given unit of time (a minute, say) is equal to a quarter of a small tank (and so an 1/8th of the big tank), then B would lose a quarter of its salt but gain an 1/8th of A’s salt. Similar equations can constructed for both A and C, giving us the following program:
from matplotlib import pyplot as plt
import numpy as np
def main():
a_salt = 1
b_salt = 1.2
c_salt = 1.3 ## initial conditions
a_salts = [a_salt]
b_salts = [b_salt]
c_salts = [c_salt]
step_count = 1500
step_size = 0.01
for _ in range(step_count):
a_salt, b_salt, c_salt = iterate(a_salt, b_salt, c_salt, step_size)
a_salts.append(a_salt)
b_salts.append(b_salt)
c_salts.append(c_salt)
plt.plot(np.arange(step_count + 1) * step_size, a_salts)
plt.plot(np.arange(step_count + 1) * step_size, b_salts)
plt.plot(np.arange(step_count + 1) * step_size, c_salts)
plt.show()
def iterate(a, b, c, step_size):
"""step all the salt levels forward"""
a += (0.25 * c - 0.125 * a) * step_size
b += (0.125 * a - 0.25 * b) * step_size
c += (0.25 * b - 0.25 * c) * step_size
return a, b, c
This is very similar to the romeo and juliette model, only with three variables. When run, it will produce a graph similar to Figure 18.3.3:
Figure 18.3.3 The amount of salt in each tank over time.
As you can see, the amounts of salt all tend towards a level where there is twice as much salt in the big tanks as the small tanks. This is because we are effectively mixing the water around, which should result in an even amount of salt per volume, which is what we see here. The specific properties of this graph are still somewhat interesting, such as the fact the tank B “overshoots” the target, resulting in a slight dip below the final resting level. This model can be extended to any number of tanks and connections, as you can see in the following exercise:
Extend the above model to a set of five tanks in a circular arrangement, with two or three connections between non-adjacent tanks. Compare how long it takes to reach equilibrium with the above model.
18.4. Conclusion
In this chapter, we scratched the surface of differential equations using a brute force approach to modeling. We started by learning about derivatives, the instantaneous rate of change of something (position, population size, etc). We used that to build the idea of a differential equation, which describes a function based on its derivative. From there, we added in systems of differential equations, which are multiple differential equations operating within the same frame of reference.
Coding this up turned out to be fairly easy, because you could iteratively solve them. The simplest example was Romeo and Juliette’s love for each other, which ended up being a pair of sine waves (turns out trig IS useful in your romantic life). We then moved on to a system in which salt water is mixed around in a closed system of tanks, and compared the characteristics of systems with more tanks to those with less.
This is all one method of understanding differential equations, and it is a useful one for a programmer. However, a slightly more conceptual explanation can be found in the previous chapter, which is also worth looking at.