25. Generating Mazes
Section author: Malcolm Smith <msmith.malcolmsmith@gmail.com>
[status: first draft]
25.1. Motivation, Prerequisites, Plan
Motivation
You have almost certainly seen a maze at least once: in a newspaper, in a classroom, wherever. On the other hand, you have almost certainly not given any thought to how that maze was made. Chances are, it was made by a computer, and in this mini-course we are going to look at the various ways you could do this yourself.
Prerequisites
The 10-hour “serious programming” course.
The “Introduction to NetworkX Graphs” mini-course in Section 24
Having the required libraries installed. Install them with:
$ pip install numpy matplotlib networkx[default]
$ sudo apt install python3-tk
Plan
To start, we will look at the definition of a maze, how we can represent it mathematically, and how that translates to code. We will then use this knowledge to implement three different maze generation algorithms, each with its own pros and cons. One important note is that there are many examples of incomplete code being shown; while you should read and undertsand it, the programs that are ready to run are always accompanied by a download button that you can run immidiately.
25.2. What is a Maze?
Before defining what a maze is, we should think about how we would want one to be. Obviously, we want there to be a path from every point to every other point, so that there aren’t any areas cut off. Technically, you could make a maze where this wasn’t the case, but the inaccessable regions might as well not be there, so for our purposes we will say that you have to be able to get from anywhere in a maze to anywhere else.
Secondly, we want there to be only one path from anywhere to anywhere else. The reasoning for this is that we want there to be exactly one solution, and having more than one path from a point to another point (for example, the start to the finish) would prevent this from being the case.
Finally, we want our maze to be in a rectangular grid. There are other forms of maze that could satisfy the other requirements, but for our purposes, a maze will be a rectangle in which there is one path from a point to any other point.
With that out of the way, let’s think about how we could rigorously represent this. It would be possible in the form that we’re used to seeing mazes in, but a form that’s easier to work with is that pathways of the maze. If that doesn’t make sense, think about it this way: currently, at a given cell in the maze, there are walls telling you where you cannot go. We want to make it so that at every cell, there is a point, and lines going to other neighboring points to tell you where you can go. If this still doesn’t feel intuitive, another way to think about it is drawing every possible path in the maze, then getting rid of the walls. A moment of thought should convince you that these two forms of maze, the walls and the pathways, give equivalent information and are interchangeable.
25.3. Representing Mazes with Python
Because the mazes will be being represent as a set of pathways through a grid, a library for representing pathways and points would be useful to us. NetworkX is such a library, and it is what we will be using for the rest of this chapter. As a quick reminder, NetworkX is a library that can store a mathematical network as a single object, allowing easy access to lots of information. We won’t use it very extensively in this chapter, though, and we will simply be adding and removing edges without doing anything fancy.
To start, let us make a simple function to create a maze without any pathways:
import numpy as np
import networkx as nx
class node(object):
"""Serves as a node in a NetworkX network, because arrays cannot"""
def __init__(self, x, y):
self.x = x
self.y = y
def gen_blank_maze(dims):
"""returns a blank grid and an array containing the nodes"""
new_maze = nx.Graph()
node_arr = []
for x in range(dims[0]):
node_arr.append([])
for y in range(dims[1]):
new_node = node(x, y)
new_maze.add_node(new_node)
node_arr[-1].append(new_node)
return new_maze, np.array(node_arr)
Before discussing what this does, note that there is something you may
not have seen before here: a class defintion. A class defines a new
type of object (in this case called a “node”), and gives it various
properties. In this case, all it does is storing the x and y of the
node, which we would normally use a list or dictionary for. However,
NetworkX throws an error if you give it a list or dictionary as a
node, so we have to use a new type of object. You don’t need to fully
understand classes; just know that when we type some_node.x or
some_node.y, we are referring to that node’s coordinates in the
maze.
The node array, or node_arr, serves a similar purpose to the node
class. It is a nested array of the nodes, arranged in such a way that
node_arr[x][y] will give the node at x, y. This may seem
redundant, and it technically is, but the ability to both find a node
given coordinates and get coordinates given a node without have to do
complex array manipulation is something we will need later
on. Currently, the maze itself is the least interesting part; it
doesn’t have any egdes, and so is just a less orderly version of the
node array. However, we will soon use the incredible versatility of
NetworkX to turn this into the set of pathways that form a
maze. Finally, note that dims is an array with the number of cells
in the x direction and the number of cells in the y direction.
25.4. Introductory Example: A Snaking Path
Before getting to the actual algorithms that can generate a random maze, let us first look at a simple script that will create a path that slowly snakes down the maze, as shown in Figure 25.4.1:
Figure 25.4.1 A trivial maze.
In order to generate this maze, we need two things: the set of pathways, which will be just one long line, and the function to convert the pathways into a recognizable maze. The second of these challenges is by far the more daunting, and what this section will focus on.
Before doing that, however, we must write the simple function to make the snaking path. This can be achieved fairly easily with:
def snaking_path(maze, node_arr):
"""turns an empty maze into a single path snaking from top to bottom"""
dims = [node_arr.shape[0], node_arr.shape[1]]
direction = 'plus x'
x = 0
y = 0
while True:
if direction == 'plus x':
# going right
if x != dims[0] - 1:
# not at the end of the row
maze.add_edge(node_arr[x][y], node_arr[x + 1][y])
x += 1
else:
# at the end of the row
if y == dims[1] - 1:
# also at the top
break
maze.add_edge(node_arr[x][y], node_arr[x][y + 1])
direction = 'minus x'
y += 1
else:
# going left
if x != 0:
# not at the end of the row
maze.add_edge(node_arr[x][y], node_arr[x - 1][y])
x -= 1
else:
# at the end of the row
if y == dims[1] - 1:
# also at the top
break
maze.add_edge(node_arr[x][y], node_arr[x][y + 1])
direction = 'plus x'
y += 1
return maze
Though it may look a bit complicated, what this program is doing is actually quite simple. It moves through the maze row by row, and then switching direction whenever it moves up a row. This is a trivial example of a maze generation algorithm, because it is not random in any way. This means it will always produce the same maze, which also happens to be incredibly easy to solve.
Moving on the function to display the maze, it gets more complex. We will look at it in blocks, so that it’s easier to understand. However, before we do that, we need to understand how you would even go about converting as set of pathways into a maze with walls. Because the pathway maze is a set of lines you can walk on, if you overlay the pathway maze on the final maze, they should never intersect. If they did, it would mean there’s a wall between two cells that are connected on the pathway maze, which means you can’t walk between them. So, our algorithm for this will be to completely fill the final maze, then remove any walls that overlap with a line in the pathway maze.
def show_wall_maze(maze, dims):
"""show the maze in a format recognizable to most people"""
dims = [dims[0] + 1, dims[1] + 1]
wall_maze, wall_node_arr = gen_blank_maze(dims)
for x in range(dims[0]):
for y in range(dims[1]):
if (x + y) % 2 == 0: # avoids doubling edges
current_node = wall_node_arr[x][y]
neighbors = unvisited_neighbors(current_node, [], wall_node_arr, dims)
for neighbor in neighbors:
wall_maze.add_edge(current_node, neighbor)
The first block is just the setup for the maze. The final maze has to
have dimensions that are one bigger than the pathway maze, because
each node in the pathway maze is at the center of a square made by
four nodes of the final maze. To verify this for yourself, imagine a
2x2 pathway maze. That corresponds to 4 cells in the final maze
(meaning little squares), and it is easy to see that to have four such
cells you would need a 3x3 grid. The next part of this is the part
labeled “avoid doubling edges”. What this does is select only a
checkerboard of nodes, as opposed to every single one. This means that
when we draw lines from every node in the checkerboard in every
direction, they will not overlap with any other lines that have
already been drawn. Finally, we have a function in here called
unvisited_neighbors(), which we will look at after getting through
this function.
for edge in maze.edges:
# this code shows the relationship between the paths in the maze and the
# edges of the maze
if edge[0].x == edge[1].x:
if edge[0].y > edge[1].y: # make sure the edge is in the right order for the formula
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x][edge[0].y + 1], wall_node_arr[edge[1].x + 1][edge[1].y]
if edge[0].y == edge[1].y:
if edge[0].x > edge[1].x:
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x + 1][edge[0].y], wall_node_arr[edge[1].x][edge[1].y + 1]
wall_maze.remove_edge(edge_to_remove[0], edge_to_remove[1])
This block is the core of this function. It runs through every edge in the pathway maze, and removes the edge that overlaps it in the final maze. As it turns out, this requires knowledge of both the edge’s orientation (horizontal or vertical) and the direction of the edge. Despite being a non-directed graph, NetworkX still keeps track of the order you put the ends of the edge in, so you have to be careful to get those in the correct order before applying the formula. The formula itself is somewhat simple: if the edge is horizontal (x’s are equal), the overlapping edge has the coordinates (x1, y1 + 1) -> (x2 + 1, y2). If it’s vertical (y’s equal), then the overlapping edge is (x1 + 1, y1) -> (x2, y2 + 1). After finding that edge, the function then removes it from the final maze.
# remove edges for the start and end
start_edge = wall_node_arr[0][0], wall_node_arr[0][1]
end_edge = wall_node_arr[dims[0] - 1][dims[1] - 1], wall_node_arr[dims[0] - 1][dims[1] - 2]
wall_maze.remove_edges_from([start_edge, end_edge])
This block is entirely stylistic, it removes two edges around the border to serve as the start and end.
# use networkx layout functions to arrange nodes in a grid
layer_dict = {}
for i in range(len(wall_node_arr)):
layer_dict[i] = wall_node_arr[i]
pos = nx.multipartite_layout(wall_maze, subset_key=layer_dict)
nx.draw(wall_maze, pos=pos, arrows=False, node_size=0, width=2)
plt.show()
This block is what finally shows the maze, using the compatibility between NetworkX and Matplotlib. Specifically, it converts the node array into a dictionary (because that’s what NetworkX uses), then uses a NetworkX feature to arrange the nodes in a grid. It then draws it, using specific parameters to make the final product look nice.
In the first block, we saw a function called
unvisited_neighbors(). This function is used by all the generation
algorithms we are going to look at, as well as the
show_wall_maze() function, so it is also worth looking at.
def unvisited_neighbors(node, nodes_visited, node_arr, dims):
"""find all the neighbors of a given node not yet visited"""
x, y = node.x, node.y
neighbors = []
# makes sure no nodes that aren't in the maze are added to the neighbors
if x != 0:
neighbors.append(node_arr[x - 1][y])
if x != dims[0] - 1:
neighbors.append(node_arr[x + 1][y])
if y != 0:
neighbors.append(node_arr[x][y - 1])
if y != dims[1] - 1:
neighbors.append(node_arr[x][y + 1])
visited_neighbors = []
for neighbor in neighbors:
if neighbor in nodes_visited:
visited_neighbors.append(neighbor)
# remove visited neighbors
neighbors = [i for i in neighbors if i not in visited_neighbors]
return neighbors
This function is quite simple, as it is just checking if the node is
against any of the walls, and then adding the appropriate nodes the
neighbors array. It also has some code at the bottom to remove any
nodes that are in an array of visited nodes, hence the name
“unvisited”. However, in this case, we passed in an empty array for
the visited nodes, so it doesn’t remove any of the neighbors.
With these three functions, along with the function to make a blank
maze we defined in the previous section, we can write a simple program
to display the snaking maze, which can be downloaded here
snaking_maze.py:
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
def main():
dims = [5, 5]
maze, node_arr = gen_blank_maze(dims)
maze = snaking_path(maze, node_arr)
show_wall_maze(maze, dims)
class node(object):
"""Serves as a node in the NetworkX network, because arrays cannot"""
def __init__(self, x, y):
self.x = x
self.y = y
def gen_blank_maze(dims):
"""returns a blank grid and an array containing the nodes"""
new_maze = nx.Graph()
node_arr = []
for x in range(dims[0]):
node_arr.append([])
for y in range(dims[1]):
new_node = node(x, y)
new_maze.add_node(new_node)
node_arr[-1].append(new_node)
return new_maze, np.array(node_arr)
def unvisited_neighbors(node, nodes_visited, node_arr, dims):
"""find all the neighbors of a given node not yet visited"""
x, y = node.x, node.y
neighbors = []
# makes sure no nodes that aren't in the maze are added to the neighbors
if x != 0:
neighbors.append(node_arr[x - 1][y])
if x != dims[0] - 1:
neighbors.append(node_arr[x + 1][y])
if y != 0:
neighbors.append(node_arr[x][y - 1])
if y != dims[1] - 1:
neighbors.append(node_arr[x][y + 1])
visited_neighbors = []
for neighbor in neighbors:
if neighbor in nodes_visited:
visited_neighbors.append(neighbor)
# remove visited neighbors
neighbors = [i for i in neighbors if i not in visited_neighbors]
return neighbors
def snaking_path(maze, node_arr):
"""turns an empty maze into a single path snaking from top to bottom"""
dims = [node_arr.shape[0], node_arr.shape[1]]
direction = 'plus x'
x = 0
y = 0
while True:
if direction == 'plus x':
# going right
if x != dims[0] - 1:
maze.add_edge(node_arr[x][y], node_arr[x + 1][y])
x += 1
else:
if y == dims[1] - 1:
break
maze.add_edge(node_arr[x][y], node_arr[x][y + 1])
direction = 'minus x'
y += 1
else:
# going left
if x != 0:
maze.add_edge(node_arr[x][y], node_arr[x - 1][y])
x -= 1
else:
if y == dims[1] - 1:
break
maze.add_edge(node_arr[x][y], node_arr[x][y + 1])
direction = 'plus x'
y += 1
return maze
def show_wall_maze(maze, dims):
"""show the maze in a format recognizable to most people"""
dims = [dims[0] + 1, dims[1] + 1]
wall_maze, wall_node_arr = gen_blank_maze(dims)
for x in range(dims[0]):
for y in range(dims[1]):
if (x + y) % 2 == 0: # avoids doubling edges
current_node = wall_node_arr[x][y]
neighbors = unvisited_neighbors(current_node, [], wall_node_arr, dims)
for neighbor in neighbors:
wall_maze.add_edge(current_node, neighbor)
for edge in maze.edges:
# this code shows the relationship between the paths in the maze and the
# edges of the maze
if edge[0].x == edge[1].x:
if edge[0].y > edge[1].y: # make sure the edge is in the right order for the formula
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x][edge[0].y + 1], wall_node_arr[edge[1].x + 1][edge[1].y]
if edge[0].y == edge[1].y:
if edge[0].x > edge[1].x:
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x + 1][edge[0].y], wall_node_arr[edge[1].x][edge[1].y + 1]
wall_maze.remove_edge(edge_to_remove[0], edge_to_remove[1])
# remove edges for the start and end
start_edge = wall_node_arr[0][0], wall_node_arr[0][1]
end_edge = wall_node_arr[dims[0] - 1][dims[1] - 1], wall_node_arr[dims[0] - 1][dims[1] - 2]
wall_maze.remove_edges_from([start_edge, end_edge])
# use networkx layout functions to arrange nodes in a grid
layer_dict = {}
for i in range(len(wall_node_arr)):
layer_dict[i] = wall_node_arr[i]
pos = nx.multipartite_layout(wall_maze, subset_key=layer_dict)
nx.draw(wall_maze, pos=pos, arrows=False, node_size=0, width=2)
plt.show()
main()
When run, this particular program will produce the exact maze you see in the image at the start of the section. I know it may have been a bit overwhelming to learn all these functions so quickly, but from now on all we have to do is code and try out the individual generation algorithms, without worrying about the superficial programs breaking on us.
25.5. Generation Algorithms
As mentioned before, we will be using three algorithms to generate mazes. The first is known as a depth-first search, and the method it uses is to randomly take steps onto nodes that haven’t previously been visited (to avoid forming loops) until it gets stuck, then retraces backwards until it finds a node it could take a step from, then repeats. This is guaranteed to hit every node exactly once, without forming loops. The disadvantage is that it can take a lot of memory for larger mazes, as it has to keep track of everywhere it’s been.
To implement this, we can add the following program to the file:
import random
def depth_first(maze, node_arr):
"""returns a set of pathways found by a depth-first search"""
path = []
nodes_visited = []
dims = [len(node_arr), len(node_arr[0])] # for convenience
current_node = node_arr[0][0] # start with arbitrarily chosen node
while len(nodes_visited) < dims[0] * dims[1] - 1:
path.append(current_node)
nodes_visited.append(current_node)
neighbors = unvisited_neighbors(path[-1], nodes_visited, node_arr, dims)
while len(neighbors) == 0: # checks if there are unvisited neighbors
path.pop(-1) # goes back along the path until a node with unvisited neighbors is found
neighbors = unvisited_neighbors(path[-1], nodes_visited, node_arr, dims)
random.shuffle(neighbors)
current_node = neighbors[0] # chooses a random neighbor
maze.add_edge(path[-1], current_node)
return maze
If you run the depth_first() function now, it will return the
completed set of pathways. To visualize this, we need to plug it in to
the function we already wrote to display a maze in the previous
section. With this final piece, we can make see the results of the
first generation algorithm, the code for which is shown in
Listing 25.5.1 and downloadable here
depth_first.py:
import numpy as np
import networkx as nx
import random
import matplotlib.pyplot as plt
def main():
dims = [5, 5]
maze, node_arr = gen_blank_maze(dims)
maze = depth_first(maze, node_arr)
save_wall_maze(maze, dims)
class node(object):
"""Serves as a node in the NetworkX network, because arrays cannot"""
def __init__(self, x, y):
self.x = x
self.y = y
def gen_blank_maze(dims):
"""returns a blank grid and an array containing the nodes"""
new_maze = nx.Graph()
node_arr = []
for x in range(dims[0]):
node_arr.append([])
for y in range(dims[1]):
new_node = node(x, y)
new_maze.add_node(new_node)
node_arr[-1].append(new_node)
return new_maze, np.array(node_arr)
def depth_first(maze, node_arr):
"""returns a set of pathways found by a depth-first search"""
path = []
nodes_visited = []
dims = [len(node_arr), len(node_arr[0])] # for convenience
current_node = node_arr[0][0] # start with arbitrarily chosen node
while len(nodes_visited) < dims[0] * dims[1] - 1:
path.append(current_node)
nodes_visited.append(current_node)
neighbors = unvisited_neighbors(path[-1], nodes_visited, node_arr, dims)
while len(neighbors) == 0: # checks if there are unvisited neighbors
path.pop(-1) # goes back along the path until a node with unvisited neighbors is found
neighbors = unvisited_neighbors(path[-1], nodes_visited, node_arr, dims)
random.shuffle(neighbors)
current_node = neighbors[0] # chooses a random neighbor
maze.add_edge(path[-1], current_node)
return maze
def unvisited_neighbors(node, nodes_visited, node_arr, dims):
"""find all the neighbors of a given node not yet visited"""
x, y = node.x, node.y
neighbors = []
# makes sure no nodes that aren't in the maze are added to the neighbors
if x != 0:
neighbors.append(node_arr[x - 1][y])
if x != dims[0] - 1:
neighbors.append(node_arr[x + 1][y])
if y != 0:
neighbors.append(node_arr[x][y - 1])
if y != dims[1] - 1:
neighbors.append(node_arr[x][y + 1])
visited_neighbors = []
for neighbor in neighbors:
if neighbor in nodes_visited:
visited_neighbors.append(neighbor)
# remove visited neighbors
neighbors = [i for i in neighbors if i not in visited_neighbors]
return neighbors
def save_wall_maze(maze, dims):
"""show the maze in a format recognizable to most people"""
dims = [dims[0] + 1, dims[1] + 1]
wall_maze, wall_node_arr = gen_blank_maze(dims)
for x in range(dims[0]):
for y in range(dims[1]):
if (x + y) % 2 == 0: # avoids doubling edges
current_node = wall_node_arr[x][y]
neighbors = unvisited_neighbors(current_node, [], wall_node_arr, dims)
for neighbor in neighbors:
wall_maze.add_edge(current_node, neighbor)
for edge in maze.edges:
# this code shows the relationship between the paths in the maze and the
# edges of the maze
if edge[0].x == edge[1].x:
if edge[0].y > edge[1].y: # make sure the edge is in the right order for the formula
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x][edge[0].y + 1], wall_node_arr[edge[1].x + 1][edge[1].y]
if edge[0].y == edge[1].y:
if edge[0].x > edge[1].x:
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x + 1][edge[0].y], wall_node_arr[edge[1].x][edge[1].y + 1]
wall_maze.remove_edge(edge_to_remove[0], edge_to_remove[1])
# remove edges for the start and end
start_edge = wall_node_arr[0][0], wall_node_arr[0][1]
end_edge = wall_node_arr[dims[0] - 1][dims[1] - 1], wall_node_arr[dims[0] - 1][dims[1] - 2]
wall_maze.remove_edges_from([start_edge, end_edge])
# use networkx layout functions to arrange nodes in a grid
layer_dict = {}
for i in range(len(wall_node_arr)):
layer_dict[i] = wall_node_arr[i]
pos = nx.multipartite_layout(wall_maze, subset_key=layer_dict)
nx.draw(wall_maze, pos=pos, arrows=False, node_size=0, width=2)
plt.savefig('depth_first.png')
print('Maze saved to depth_first.png')
plt.show()
main()
When run, this will display a maze, as well as saving it to a file. The maze should look something like Figure 25.5.1:
Figure 25.5.1 A very simple maze.
You can try increasing the dimensions in the main() function, and
you should see that it still runs fairly fast. However, the amount of
memory it takes can increase considerably as the maze gets bigger. The
next algorithm we will look at has the opposite set of problems: slow
runtime, but not a lot of memory. It’s called hunt and kill, the
reason for which we will soon see.
Hunt and kill initially works the same way as depth first search, but when it gets stuck, instead of retracing its steps, it starts searching from the top down, row by row, until it finds a node that has already been visited with an unvisited neighbor, then repeats. This is also guaranteed to completely fill the maze, because it won’t stop looking through the maze until it hits every node. To implement this, we can add the following function to the program:
def hunt_kill(maze, node_arr):
"""generate maze pathways via the hunt and kill algorithm"""
nodes_visited = []
dims = [len(node_arr), len(node_arr[0])]
current_node = node_arr[0][0]
while len(nodes_visited) < dims[0] * dims[1] - 1:
nodes_visited.append(current_node)
previous_node = [current_node].copy()[0]
neighbors = unvisited_neighbors(previous_node, nodes_visited, node_arr, dims)
if len(neighbors) == 0: # checks if there are unvisited neighbors
for x in range(dims[0]):
for y in range(dims[1]):
previous_node = node_arr[x][y]
if previous_node in nodes_visited:
# finds a node that has been visited and has unvisited neighbors
neighbors = unvisited_neighbors(previous_node, nodes_visited, node_arr, dims)
if len(neighbors) != 0:
break
if len(neighbors) != 0:
break
random.shuffle(neighbors)
current_node = neighbors[0]
maze.add_edge(previous_node, current_node)
return maze
Replacing the depth_first() in main() with hunt_kill() is
all you need to do now, and the program should produce more mazes
similar to the ones from depth_first(). This modified progran can
be downloaded here hunt_kill.py. However, if the size is
increased to a reasonable degree, the runtime will increase
significantly. The upside to the algorithm, though, is that the memory
will stay low throughout the process, though there is not an easy way
to see this.
The third and final algorithm we will look at is the most interesting. It’s called origin shift, and it uses a property of mathematical trees to work. For those who don’t know, a tree is a special type of mathematical network where there is exactly one path from any point to any other point. If that sounds familiar, it’s because that’s the same definition we gave to the set of pathways of a maze. This means any type of theory related to trees can be applied to our maze. In this case, we will use something called a rooted tree. For a tree to be rooted, the network needs to be directed, so we’ll start by adding a line to make the maze directed:
...
maze = nx.DiGraph(maze)
...
Now, the way origin shift works. It’s actually a method for modifying a maze while making sure it’s still a maze, but can also be used to generate one, as we will soon see. To start, you choose a random point in the maze (we are going to use 0, 0 for convenience). That point is your root. To make a point the root, imagine all paths to it, then point those edges toward the root. Another way to think about it is, at every point, look for the point that would take you closer to the root, then draw an arrow towards it. After doing this, you will have a rooted tree.
A property of rooted trees is that every node has exactly one arrow going out of it, except the root, which has none. We can use this property to our advantage by ensuring that these properties always hold, no matter where the root is. To move the root, and consequently make an update to the maze, simply choose a random direction for the root to move in (that is, up, down, left, or right), and move it in that direction. To make sure it is still the root, draw an arrow from the old root to the new one (because of the way you draw arrows to get to the root), then remove the outgoing arrow from the new root. This works because it redirects everything from the old root to the new one, and makes sure that the new root doesn’t have any outgoing arrows. With those conditions satisfied, it is still a rooted tree, meaning it is still a tree, which means it is still a valid maze.
To make this into a maze generation algorithm, as opposed to a maze update one, we can start with a simple tree, and then run the algorithm many times on it. If you save it in real time, you can also see the maze updating, which is somewhat mesmerizing. Note that the input to the origin shift function will have to be a tree. Because it outputs a tree, and we are going to be starting with a tree, we don’t have to worry about that in this case, but it is important to note if you want to use it for anything else. With that being said, here is the complete origin shift function:
def origin_shift(maze, node_arr, n_iterations): # note: edges must already be pointed to root.
"""uses the origin shift algorithm to generate a maze"""
maze = simple_tree(maze, node_arr)
root = node_arr[0][0]
dims = [len(node_arr), len(node_arr[0])]
for i in range(n_iterations):
root_neighbors = unvisited_neighbors(root, [], node_arr, dims)
random.shuffle(root_neighbors)
old_root = root
root = root_neighbors[0]
maze.add_edge(old_root, root)
# removes the outgoing edge from the new root
maze.remove_edge(list(maze.out_edges(root))[0][0],list(maze.out_edges(root))[0][1])
if i % 10 == 0:
# save the maze every 10 iterations
save_wall_maze(maze, dims, show_fig=False)
return maze
Remarkably, despite this being the most conceptually complex generation algorithm, the code for it is the simplest of the three. There are a couple reasons for this, but the main one is that the rules you need to follow to actually implement it are quite simple. Because the theory behind it is somewhat complex, I would recommend trying a couple of small examples to prove to yourself that it works:
Try making a couple small sets of pathways for a maze, and applying origin shift to them. See for yourself that there will still always be exactly one path from any point to any other point after applying the algorithm any number of times. Also: while we make the root move in a random walk for convenience, moving it from place to place randomly will also work.
For the above code to work, you will also need to add a little to the
save_wall_maze() function to make sure it doesn’t pop up a
Matplotlib figure every 10 iterations:
def save_wall_maze(maze, dims, show_fig=True):
...
...
# remove plt.show() and replace it with:
if show_fig:
plt.show()
else:
plt.clf()
We will also, of course, need a function to generate the simple tree. This is also where we will convert the maze to a direct graph:
def simple_tree(maze, node_arr): # assumes maze is empty
"""returns the simplest possible tree given the starting maze"""
maze = nx.DiGraph(maze)
dims = [len(node_arr), len(node_arr[0])]
for x in range(dims[0]):
if x != dims[0] - 1:
maze.add_edge(node_arr[x + 1][0], node_arr[x][0])
for y in range(dims[1] - 1):
maze.add_edge(node_arr[x][y + 1], node_arr[x][y])
return maze
With all of that, let us make a new program using most of the same
helper functions from the previous one in Listing 25.5.2,
which can be downloaded here origin_shift.py:
import numpy as np
import networkx as nx
import random
import matplotlib.pyplot as plt
def main():
dims = [25, 25]
iterations = 5000
maze, node_arr = gen_blank_maze(dims)
maze = origin_shift(maze, node_arr, iterations)
save_wall_maze(maze, dims)
class node(object):
"""Serves as a node in the NetworkX network, because arrays cannot"""
def __init__(self, x, y):
self.x = x
self.y = y
def gen_blank_maze(dims):
"""returns a blank grid and an array containing the nodes"""
new_maze = nx.Graph()
node_arr = []
for x in range(dims[0]):
node_arr.append([])
for y in range(dims[1]):
new_node = node(x, y)
new_maze.add_node(new_node)
node_arr[-1].append(new_node)
return new_maze, np.array(node_arr)
def simple_tree(maze, node_arr): # assumes maze is empty
"""returns the simplest possible tree given the starting maze"""
maze = nx.DiGraph(maze)
dims = [len(node_arr), len(node_arr[0])]
for x in range(dims[0]):
if x != dims[0] - 1:
maze.add_edge(node_arr[x + 1][0], node_arr[x][0])
for y in range(dims[1] - 1):
maze.add_edge(node_arr[x][y + 1], node_arr[x][y])
return maze
def origin_shift(maze, node_arr, n_iterations): # note: edges must already be pointed to root.
"""uses the origin shift algorithm to generate a maze"""
maze = simple_tree(maze, node_arr)
root = node_arr[0][0]
dims = [len(node_arr), len(node_arr[0])]
for i in range(n_iterations):
root_neighbors = unvisited_neighbors(root, [], node_arr, dims)
random.shuffle(root_neighbors)
old_root = root
root = root_neighbors[0]
maze.add_edge(old_root, root)
# removes the outgoing edge from the new root
maze.remove_edge(list(maze.out_edges(root))[0][0],list(maze.out_edges(root))[0][1])
if i % 10 == 0:
# save the maze every 10 iterations
save_wall_maze(maze, dims, show_fig=False)
return maze
def unvisited_neighbors(node, nodes_visited, node_arr, dims):
"""find all the neighbors of a given node not yet visited"""
x, y = node.x, node.y
neighbors = []
# makes sure no nodes that aren't in the maze are added to the neighbors
if x != 0:
neighbors.append(node_arr[x - 1][y])
if x != dims[0] - 1:
neighbors.append(node_arr[x + 1][y])
if y != 0:
neighbors.append(node_arr[x][y - 1])
if y != dims[1] - 1:
neighbors.append(node_arr[x][y + 1])
visited_neighbors = []
for neighbor in neighbors:
if neighbor in nodes_visited:
visited_neighbors.append(neighbor)
# remove visited neighbors
neighbors = [i for i in neighbors if i not in visited_neighbors]
return neighbors
def save_wall_maze(maze, dims, show_fig=True):
"""show the maze in a format recognizable to most people"""
dims = [dims[0] + 1, dims[1] + 1]
wall_maze, wall_node_arr = gen_blank_maze(dims)
for x in range(dims[0]):
for y in range(dims[1]):
if (x + y) % 2 == 0: # avoids doubling edges
current_node = wall_node_arr[x][y]
neighbors = unvisited_neighbors(current_node, [], wall_node_arr, dims)
for neighbor in neighbors:
wall_maze.add_edge(current_node, neighbor)
for edge in maze.edges:
# this code shows the relationship between the paths in the maze and the
# edges of the maze
if edge[0].x == edge[1].x:
if edge[0].y > edge[1].y: # make sure the edge is in the right order for the formula
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x][edge[0].y + 1], wall_node_arr[edge[1].x + 1][edge[1].y]
if edge[0].y == edge[1].y:
if edge[0].x > edge[1].x:
edge = list(reversed(edge))
edge_to_remove = wall_node_arr[edge[0].x + 1][edge[0].y], wall_node_arr[edge[1].x][edge[1].y + 1]
wall_maze.remove_edge(edge_to_remove[0], edge_to_remove[1])
# remove edges for the start and end
start_edge = wall_node_arr[0][0], wall_node_arr[0][1]
end_edge = wall_node_arr[dims[0] - 1][dims[1] - 1], wall_node_arr[dims[0] - 1][dims[1] - 2]
wall_maze.remove_edges_from([start_edge, end_edge])
# use networkx layout functions to arrange nodes in a grid
layer_dict = {}
for i in range(len(wall_node_arr)):
layer_dict[i] = wall_node_arr[i]
pos = nx.multipartite_layout(wall_maze, subset_key=layer_dict)
nx.draw(wall_maze, pos=pos, arrows=False, node_size=0, width=2)
plt.savefig('origin_shift.png')
print('Maze saved to origin_shift.png')
if show_fig:
plt.show()
else:
plt.clf()
main()
With the current variables in main(), this will run extremely
quickly. Normally, this is a good thing, but to see how the maze
updates over time, we want it slower. In addition, a larger maze with
make the random walk effect of this program more apparent. Try running
it with dims = [25, 25] and iterations = 5000. It should take
significantly longer to run, and allow you to see the maze changing in
real time. This will produce, as you might have guessed from the
dimensions, a significantly larger maze (such as the one pictured in
Figure 25.5.2) than the programs we have run so
far.
Figure 25.5.2 A larger maze generated with the origin shift algorithm.
Something else that may have been apparent is why we needed so many iterations: the direction the root moves is entirely random, so there’s always the chance that it misses an entire region and leaves it as rows of vertical lines. This brings us to the shape of the simple tree, which is pictured in Figure 25.5.3:
Figure 25.5.3 The shape of the simple tree.
This graph doesn’t have arrows, but the root is in the bottom left, and it’s easy to see how all the arrows point to it: vertical lines point down, horizontal ones point left. This is why the graph is so vertical at first as well. There are some steps you could take to optimize the algorithm to take fewer iterations, but for our purposes a completely random walk is good enough.
25.6. Interactive Mazes
Now that we have algorithms to generate and display mazes, we will add features to make them interactive. To do this, we will be using the tkinter library instead of matplotlib, meaning we will need to code the presentation of the maze manually. Tkinter is a python library used for visual applications of python, and gathering user input through GUI. You don’t need a deep understanding of this library to show a maze like this; however, some of the basics are necessary. The main features we will be using are:
tk.Tk()- creates the main tkinter object that can be displayed.tk.Canvas()- creates a canvas that can have shapes drawn on it.tk.Frame()- creates an area of the window to hold buttons and other widgets.tk.Button()- creates a clickable button that executes code when pressed.tk.Tk().mainloop()- displays the window with the widgets and parameters specified earlier.
Drawing a maze with tkinter shouldn’t be too hard; just draw lines
based on the node’s x and y coordinates, scaled by some values based
on the size of the maze. Here is a simple algorithm to replace certain
parts of the save_wall_maze() function:
def show_tkinter_maze(maze, node_arr)
"""display an interactive and solveable maze"""
dims = [node_arr.shape[0], node_arr.shape[1]]
...
...
end_edge = wall_node_arr[dims[0] - 1][dims[1] - 1], wall_node_arr[dims[0] - 1][dims[1] - 2]
wall_maze.remove_edges_from([start_edge, end_edge])
path = [(0,0)]
root = tk.Tk()
canvas = tk.Canvas(root, width=600, height=600, bg='white')
root.title('Interactive Maze')
root.minsize(600, 650)
canvas.pack()
frame = tk.Frame(root)
frame.pack(side=tk.BOTTOM)
scale = [560 / dims[0], 560 / dims[1]] # leave 30 pix buffer
border_width = max(scale) / 25
canvas.create_rectangle(30 + border_width * 5, 30 + border_width * 5, 30 + scale[0] - border_width * 5, 30 + scale[1] - border_width * 5, fill='#00008B', width=0)
tk.Button(frame, text='UP', font='comicsans 12 bold', command=lambda: move_up(maze, node_arr, path, canvas, scale)).pack(side=tk.RIGHT, pady=5,padx=5)
tk.Button(frame, text='DOWN', font='comicsans 12 bold', command=lambda: move_down(maze, node_arr, path, canvas, scale)).pack(side=tk.RIGHT,pady=5,padx=5)
tk.Button(frame, text='LEFT', font='comicsans 12 bold', command=lambda: move_left(maze, node_arr, path, canvas, scale)).pack(side=tk.RIGHT,pady=5,padx=5)
tk.Button(frame, text='RIGHT', font='comicsans 12 bold', command=lambda: move_right(maze, node_arr, path, canvas, scale)).pack(side=tk.RIGHT,pady=5,padx=5)
tk.Button(frame, text='BACK', font='comicsans 12 bold', command=lambda: back(maze, node_arr, path, canvas, scale)).pack(side=tk.RIGHT,pady=5,padx=5)
for edge in wall_maze.edges:
canvas.create_line(edge[0].x * scale[0] + 30, edge[0].y * scale[1] + 30, edge[1].x * scale[0] + 30, edge[1].y * scale[1] + 30, fill='black', width=border_width)
root.mainloop()
Notice that we have two mazes and two node arrays here: one for the
pathways, another for the walls. This can make thinking about the
specific coordinates of any given line or shape hard, so be careful
when modifying this code. For now, ignore the buttons, as we haven’t
defined the functions they will be calling yet. What this is doing is
defining a couple relavent variables, such as border_width and
scale, then drawing lines where there are edges in the wall
maze. We are also drawing a dark blue square in the starting position
to indicate where we are ('#00008B' is hexcode for dark
blue). Then, we use root.mainloop() to display the whole thing,
with a line of buttons at the bottom, as seen in
Figure 25.6.1:

Figure 25.6.1 A maze, ready for interaction to be applied.
The next step, then, is to define the functions that allow us to
interact with the maze. As you may have guessed from the button names,
we are going to have five buttons: four for the directions, and one to
undo the previous move. For stylistic reasons, the rectangles to
indicate the path are significantly smaller than the cells they
occupy. This means, in the following five functions, border_width
represents the border between the colored area and the cell wall, not
the width of the border of the cell.
def move_down(maze, node_arr, path, canvas, scale):
"""move downward on the maze"""
current_pos = path[-1]
if current_pos[1] != node_arr.shape[1] - 1:
next_pos = (current_pos[0], current_pos[1] + 1)
if (node_arr[current_pos], node_arr[next_pos]) in maze.edges:
path.append(next_pos)
border_width = max(scale) / 5
current_center = [node_arr[current_pos].x * scale[0] + 30 + scale[0] / 2, node_arr[current_pos].y * scale[1] + 30 + scale[1] / 2]
next_center = [current_center[0], current_center[1] + scale[1]]
canvas.create_rectangle(current_center[0] - scale[0] / 2 + border_width, current_center[1] - scale[1] / 2 + border_width, current_center[0] + scale[0] / 2 - border_width, current_center[1] + scale[1] / 2 - border_width, fill='#ADD8E6', width=0)
canvas.create_rectangle(next_center[0] - scale[0] / 2 + border_width, next_center[1] - scale[1] / 2 + border_width, next_center[0] + scale[0] / 2 - border_width, next_center[1] + scale[1] / 2 - border_width, fill='#00008B', width=0)
def move_up(maze, node_arr, path, canvas, scale):
"""move upward on the maze"""
current_pos = path[-1]
if current_pos[1] != 0:
next_pos = (current_pos[0], current_pos[1] - 1)
if (node_arr[current_pos], node_arr[next_pos]) in maze.edges:
path.append(next_pos)
border_width = max(scale) / 5
current_center = [node_arr[current_pos].x * scale[0] + 30 + scale[0] / 2, node_arr[current_pos].y * scale[1] + 30 + scale[1] / 2]
next_center = [current_center[0], current_center[1] - scale[1]]
canvas.create_rectangle(current_center[0] - scale[0] / 2 + border_width, current_center[1] - scale[1] / 2 + border_width, current_center[0] + scale[0] / 2 - border_width, current_center[1] + scale[1] / 2 - border_width, fill='#ADD8E6', width=0)
canvas.create_rectangle(next_center[0] - scale[0] / 2 + border_width, next_center[1] - scale[1] / 2 + border_width, next_center[0] + scale[0] / 2 - border_width, next_center[1] + scale[1] / 2 - border_width, fill='#00008B', width=0)
def move_right(maze, node_arr, path, canvas, scale):
"""move rightward on the maze"""
current_pos = path[-1]
if current_pos[0] != node_arr.shape[0] - 1:
next_pos = (current_pos[0] + 1, current_pos[1])
if (node_arr[current_pos], node_arr[next_pos]) in maze.edges:
path.append(next_pos)
border_width = max(scale) / 5
current_center = [node_arr[current_pos].x * scale[0] + 30 + scale[0] / 2, node_arr[current_pos].y * scale[1] + 30 + scale[1] / 2]
next_center = [current_center[0] + scale[0], current_center[1]]
canvas.create_rectangle(current_center[0] - scale[0] / 2 + border_width, current_center[1] - scale[1] / 2 + border_width, current_center[0] + scale[0] / 2 - border_width, current_center[1] + scale[1] / 2 - border_width, fill='#ADD8E6', width=0)
canvas.create_rectangle(next_center[0] - scale[0] / 2 + border_width, next_center[1] - scale[1] / 2 + border_width, next_center[0] + scale[0] / 2 - border_width, next_center[1] + scale[1] / 2 - border_width, fill='#00008B', width=0)
def move_left(maze, node_arr, path, canvas, scale):
"""move leftward on the maze"""
current_pos = path[-1]
if current_pos[0] != 0:
next_pos = (current_pos[0] - 1, current_pos[1])
if (node_arr[current_pos], node_arr[next_pos]) in maze.edges:
path.append(next_pos)
border_width = max(scale) / 5
current_center = [node_arr[current_pos].x * scale[0] + 30 + scale[0] / 2, node_arr[current_pos].y * scale[1] + 30 + scale[1] / 2]
next_center = [current_center[0] - scale[0], current_center[1]]
canvas.create_rectangle(current_center[0] - scale[0] / 2 + border_width, current_center[1] - scale[1] / 2 + border_width, current_center[0] + scale[0] / 2 - border_width, current_center[1] + scale[1] / 2 - border_width, fill='#ADD8E6', width=0)
canvas.create_rectangle(next_center[0] - scale[0] / 2 + border_width, next_center[1] - scale[1] / 2 + border_width, next_center[0] + scale[0] / 2 - border_width, next_center[1] + scale[1] / 2 - border_width, fill='#00008B', width=0)
def back(maze, node_arr, path, canvas, scale):
"""undo the previous move"""
current_pos = path[-1]
next_pos = path[-2]
border_width = max(scale) / 5
current_center = [node_arr[current_pos].x * scale[0] + 30 + scale[0] / 2, node_arr[current_pos].y * scale[1] + 30 + scale[1] / 2]
next_center = [node_arr[next_pos].x * scale[0] + 30 + scale[0] / 2, node_arr[next_pos].y * scale[1] + 30 + scale[1] / 2]
if path.count(current_pos) == 1:
# check if this is the last time we have been over this position
canvas.create_rectangle(current_center[0] - scale[0] / 2 + border_width, current_center[1] - scale[1] / 2 + border_width, current_center[0] + scale[0] / 2 - border_width, current_center[1] + scale[1] / 2 - border_width, fill='white', width=0)
else:
canvas.create_rectangle(current_center[0] - scale[0] / 2 + border_width, current_center[1] - scale[1] / 2 + border_width, current_center[0] + scale[0] / 2 - border_width, current_center[1] + scale[1] / 2 - border_width, fill='#ADD8E6', width=0)
canvas.create_rectangle(next_center[0] - scale[0] / 2 + border_width, next_center[1] - scale[1] / 2 + border_width, next_center[0] + scale[0] / 2 - border_width, next_center[1] + scale[1] / 2 - border_width, fill='#00008B', width=0)
path.pop(-1)
The entire interactive maze program can be downloaded here
interactive_maze.py.
This is a lot of code, but most of it is just repeated; the four
movement functions only have a couple characters differing between
them, and the back function still follows the same basic
structure. The logic of these functions is to check if you can move in
a given direction (are you at the edge of the maze, or is there a wall
in the way?), then move in that direction and draw a dark blue
rectangle where you are now and a light blue one (hexcode:
'#ADD8E6') where you were last time. Note that it never actually
removes the old rectangles, but merely draws new ones on top of
them. This in theory could hurt performance, but because we are
operating at relatively small resolutions, it should not matter all
too much.
Because we have only been modifying the function that displays the maze and adding functions, you can use any of the three algorithms to generate the maze. The maze shown earlier in this section used the depth first search algorithm, but that was an arbitrary choice.
With that said, let us run the final program. You should add the
movement functions below the show_tkinter_maze() but above the
main() call, and then running this program should create a fully
functional interactive maze, such as is shown in
Figure 25.6.2:
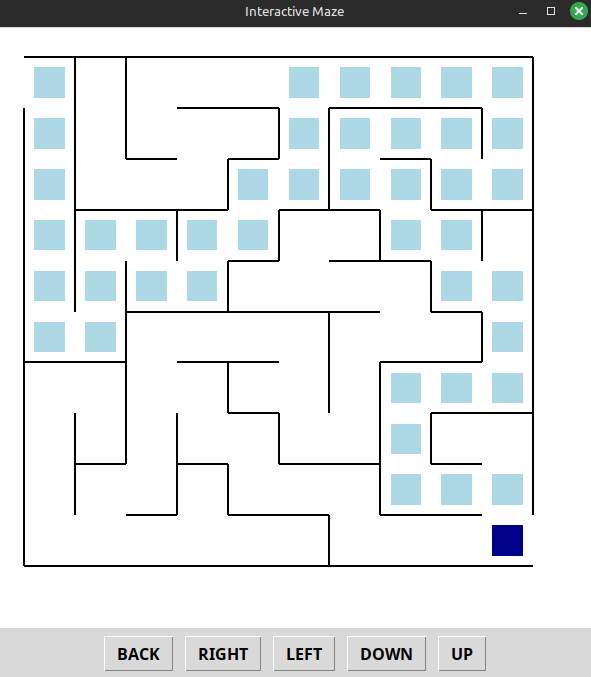
Figure 25.6.2 A 10x10 maze being solved.
This program is very resilient, and all you need to do to change the
final size of the maze is change the dimensions in the main()
function. These mazes are simple for small dimensions, but can quickly
get devilishly complex for even slightly higher ones. Before getting
to the conclusion, though, here is an exercise to get a firmer grasp
on the structure of the maze:
The current program, of course, has no built in solver. Given everything we learned about the structure of mazes, representing them as pathways, etc., what would be your algorithm for solving a maze like this? (Hint: think about the way you would solve a large maze.) (Another hint: the inclusion of a back button was not arbitrary.)
Hopefully, having a maze generator to test your own process will help with the exercise.
25.7. Conclusion
In this chapter, we discussed three (of many) maze generation algorithms. To do this, we first looked a trivial example of a generation algorithm, along with a detailed explanation of what the helper functions were doing. We then moved on to the generation algorithms, which were depth-first search, hunt and kill, and origin shift.
First, we discussed the depth first search algorithm for maze generation, which is likely the one you would want to use for generating larger mazes. It works by randomly drawing lines until it gets stuck, then retracing its steps until it is no longer stuck.
The next algorithm was very similar, though a little simpler. The hunt and kill algorithm works by drawing lines randomly until it gets stuck, then scanning each node, row by row, until it finds one that it can draw a line from, and going from there.
The last algorithm we discussed was origin shift, which is by far the most complex, at least conceptually. It works by randomly rearranging a maze while also ensuring that it’s always a valid maze, which is an interesting feat. This particular algorithm I could see having useful video game applications, such as for an ever changing maze. Regardless, it’s an incredible algorithm that deserves being looked into further than I could describe here.
Finally, we made interactive mazes with the tkinter library, a tool used to create user interfaces with python. The mazes we generated previously we could now try to solve, and verify firsthand that the algorithms worked.