12. Randomness and Disorder

[status: content-mostly-written]

Purpose: to drive home the notion of disorder (and order) and how that relates to the probabilities of various situations.

Prerequisites:

The basic Python course.
Familiarity with simple plotting.

12.1. Experiment: burn a match

NOTE: this experiment should be carried out under adult supervision.

Have a flat piece of metal, or a tile, or a very flat rock. Lay it down in a stable place.
Light a match and before the flame reaches your finger, lay it gently on the flat metal or tile or rock.
Watch it until it finishes burning and let it cool down.
If possible, take the dark stick that is left and remake it into the original match.

12.2. Experiment: ink in water

Find an ink-like substance.
Fill a discardable plastic cup with water.
Drop a single drop of the ink into the water.
Observe the ink in the water the instant it falls in.
Observe the ink in the water after thirty seconds.
If possible, make the water return the drop of ink to where it was the instant it fell in.

12.3. Discussion on “ink in water” experiment

Discuss the meaning of the “ink in water” experiment with your partners. In particular discuss the meaning of the last step and whether it was possible.

12.4. Flipping a single coin

Take a coin and flip it 16 times. Tabulate the results like this:

H T T H H H T H T T H H T H T H ...

and so forth. Count how many times you get heads and how many times you get tails.

If you use 1 for heads and 0 for tails, calculate the average of all the tosses. In the few flips shown above it will be 0.5625: just a bit more than half of the tosses were heads.

12.5. Review: random numbers in Pythyon

To review random numbers, open the python interpreter with

$ python3
>>> import random
>>> random.random()
## repeat that many times
>>> random.randint(-3, 12)
>>> random.randint(-3, 12)
## repeat that many times
>>> random.randint(0, 1)
## repeat that many times

12.6. Experiment: flipping a single virtual coin

12.6.1. Just the flips

Flipping coins just a few times can give inconsistent results. Let us explore how long it takes for the average number of heads and tails to become consistent.

In this experiment we will write a computer program to flip a single virtual coin and look at the results. Then we will update the program to keep track of the average between heads and tails. We will count heads as 1, tails as 0, and print the average as we keep flipping. First enter (or paste) the program in Listing 12.6.1.

Listing 12.6.1 single_coin_average.py

#! /usr/bin/env python3
import random

def main():
    n_runs = 16
    n_heads = 0
    n_tails = 0
    for i in range(n_runs):
        this_flip = random.randint(0, 1)
        if this_flip == 0:
            n_tails += 1
        else:
            n_heads += 1
        average = float(n_heads)/(n_heads + n_tails)
        print('%d    %f' % (i, average))

main()

Run this program with:

$ python3 single_coin_average.py
[... there will be output here ...]
$ python3 single_coin_average.py > coin_avg.dat

Then plot the results with:

$ gnuplot
# and at the gnuplot> prompt:
plot 'coin_avg.dat' using 1:2 with linespoints
plot [] [0:1] 'coin_avg.dat' using 1:2 with linespoints

Then change n_runs to be 100 and re-run the program and re-plot the results. Then plot 1000 runs.

12.6.2. Long-running average of single coin flips

Write the program in Listing 12.6.2 in a file called single_coin_flip.py

Listing 12.6.2 single_coin_flip.py

#! /usr/bin/env python3
import random

def main():
    n_runs = 16
    n_heads = 0
    n_tails = 0
    for i in range(n_runs):
        this_flip = random.randint(0, 1)
        print('%d    %d' % (i, this_flip))

main()

then run it with with:

$ python3 single_coin_flip.py
[... there will be output here ...]
$ python3 single_coin_average.py > coin_avg.dat

Then plot the results with:

$ gnuplot
# and at the gnuplot> prompt:
plot 'coin_avg.dat' using 1:2 with linespoints pt 7 ps 1

Then change n_runs to be 100 and re-run the program and re-plot the results. Then plot 1000 runs.

12.7. Flipping multiple coins

Take two different coins and flip them 16 times. Tabulate the results like this:

H T
T H
T T
H H
...

and so forth. Count how many times you get all heads and how many times you get all tails.

Do the same thing with three coins.

12.8. Experiment: flipping virtual coins

Since the purpose of computers is to automate repetitive tasks, we should not go beyond flipping three coins. Rather, we will write a computer program to do so. Enter the program in Listing 12.8.1 as many_coins.py:

Listing 12.8.1 many_coins.py

#! /usr/bin/env python3

"""
A simple program to simulate the flipping of several coins.  You
can experiment by chaning the variables n_runs and n_coins below.
"""

import random

def main():
    n_runs = 16
    n_coins = 1

    n_heads = 0
    n_tails = 0
    n_all_heads = 0
    n_all_tails = 0
    # outer loop is on how many runs we are doing
    for i in range(n_runs):
        this_flip = [0] * n_coins # store the results of a single run
        # now flip a bunch of coins for this run
        for coin in range(n_coins):
            flip = random.randint(0, 1)
            this_flip[coin] = flip
            if flip == 0:
                n_heads = n_heads + 1
            else:
                n_tails = n_tails + 1
            print('%s ' % ('H' if flip == 1 else 'T'), end="")
        if this_flip.count(0) == n_coins:
            n_all_tails = n_all_tails + 1
        if this_flip.count(1) == n_coins:
            n_all_heads = n_all_heads + 1
        print('')
    print('after %d flips of %d coins, we got the following:'
          % (n_runs, n_coins))
    print('HEADS: %d' % n_heads)
    print('TAILS: %d' % n_tails)
    print('TOTAL: %d' % (n_heads + n_tails))
    print('RUNS_WITH_ALL_HEADS: %d' % n_all_heads)
    print('RUNS_WITH_ALL_TAILS: %d' % n_all_tails)
    print('fraction_runs_all_heads: %f' % (float(n_all_heads)/n_runs))
    print('fraction_runs_all_tails: %f' % (float(n_all_tails)/n_runs))


main()

The variables at the top, n_runs and n_coins, set how many runs you do and how many coins you flip in each run.

Experiment with n_coins = 2 and try to let n_runs go through 16, 50, and then try 1000. Run the program several times with each value of n_runs and pay close attention to the output lines fraction_all_heads and fraction_all_tails – are they more consistent when n_runs is larger?

Do the same with n_coins set to 3, 4, 5, and then to 20, keeping n_runs at 1000.

Discuss what you see happen to fraction_all_heads and fraction_all_tails.

12.9. Experiment: back to physical coins - disorder

Take 10 coins, set them up to be all heads and near each other on the ground.
Take a spatula, slide it under the 10 coins, toss them high up in the air.
Watch the debris and count heads and tails.
Take the spatula again and use a single movement of the spatula to put all the 10 coins back into their original state (all near each other and all heads). If you cannot do this with a single movement of the spatula, give yourself 10 spatula moves.
Repeat this experiment with the 10 coins stacked up instead “near each other”.
Now do what you have to do to restore the 10 coins to the pile where they are all “heads up” using the spatula. I that fails, do so with your fingers.

12.10. The drunk fencer

Let us now start talking about random walks. I want to move toward discussing random walks in 2 dimensions, but it is easier to program a one-dimensional random lurching back and forth - the way a drunk fencer might move back and forth randomly rather than according to the needs of the bout.

Let us type in the program in Listing 12.10.1:

Listing 12.10.1 walk-1d.py – simulates a drunken fencer

#! /usr/bin/env python3

import random
import math
import sys

def main():
    x = 0
    n_steps = 10
    if len(sys.argv) == 2:
        n_steps = int(sys.argv[1])
    take_walk(x, n_steps)

def take_walk(x, n_steps):
    print(f'##COMMENT: sys.argv[0] - one dimensional random walk program')
    print(f'##TOTAL_STEPS_REQUESTED: {n_steps}')
    print(f'##COLUMNS: step_number, pos_x, sqrt(step_number), delta_pos_sqrt')
    for i in range(n_steps):
        ## generate a step of -1 or +1 in the x direction
        step_x = random.randint(0, 1) * 2 - 1
        x = x + step_x
        delta_x_sqrt_i = math.fabs(math.fabs(x) - math.sqrt(i))
        if i == 0:
            delta_x_sqrt_i_normalized = 0
        else:
            delta_x_sqrt_i_normalized = delta_x_sqrt_i / math.sqrt(i)
        print(i, x, math.sqrt(i), delta_x_sqrt_i, delta_x_sqrt_i_normalized)

main()

and run it and plot the results like this:

$ python3 walk-1d.py
$ python3 walk-1d.py > walk-1d.dat
$ gnuplot
# and at the gnuplot> prompt:
set grid
set size square
plot 'walk-1d.dat' using 1:2 with lines

By changing the number of steps to 100, 1000 and 10000 you should see the plots in Figure 12.10.1.

../_images/walk-path-1d.svg — Figure 12.10.1 The path of a drunken fencer 100, 1000, 10000 and 100000 steps.

12.11. The drunkard’s walk

Now we move on to the more gratifying 2-dimensional random walk, also called the drunkard’s walk.

First introduce the notion with pictures and possibly an acting out of drunk behavior. Then type in the program in Listing 12.11.1

Listing 12.11.1 walk.py

#! /usr/bin/env python3

import random
import math
import sys

def main():
    x = 0
    y = 0
    n_steps = 10
    if len(sys.argv) == 2:
        n_steps = int(sys.argv[1])
    take_walk(x, y, n_steps)

def take_walk(x, y, n_steps):
    print(f'##COMMENT: sys.argv[0] - two dimensional random walk program')
    print(f'##TOTAL_STEPS_REQUESTED: {n_steps}')
    print(f'##COLUMNS: step_number, pos_x, pos_y, distance_from_origin')
    for i in range(n_steps):
        ## generate steps of -1 or +1 in x and y directions
        step_x = 0
        step_y = 0
        ## use a coin toss to decide if we go in the x or y direction
        if random.randint(0, 1) == 0:
            step_x = random.randint(0, 1) * 2 - 1
        else:
            step_y = random.randint(0, 1) * 2 - 1
        x = x + step_x
        y = y + step_y
        distance = math.sqrt(x*x + y*y) # distance from the origin
        print(i, x, y, distance)
        ## NOTE: if you want you can go farther and explore the way
        ## average distance scales with the number of steps (should be
        ## proprtional to the square root of the number of steps).
        ## for this it might be interesting to also print math.sqrt(i)

main()

Examples of running this program:

$ python3 walk.py
$ python3 walk.py 20
$ python3 walk.py 100

Now we want to do a big run and save the data to a file:

$ python3 walk.py 1000000 > walk-1000000.dat

Now we plot it. Note the tricks with the tail command which let you plot just the first few lines rather than the whole file:

$ gnuplot
# and at the gnuplot> prompt:
set grid
set size square
plot '<tail -100 walk-1000000.dat' using 2:3 with lines
plot '<tail -1000 walk-1000000.dat' using 2:3 with lines
plot '<tail -10000 walk-1000000.dat' using 2:3 with lines
plot '<tail -100000 walk-1000000.dat' using 2:3 with lines
plot '<tail -1000000 walk-1000000.dat' using 2:3 with lines

By changing the number of steps to 100, 1000 and 10000 you should see the plots in Figure 12.11.1

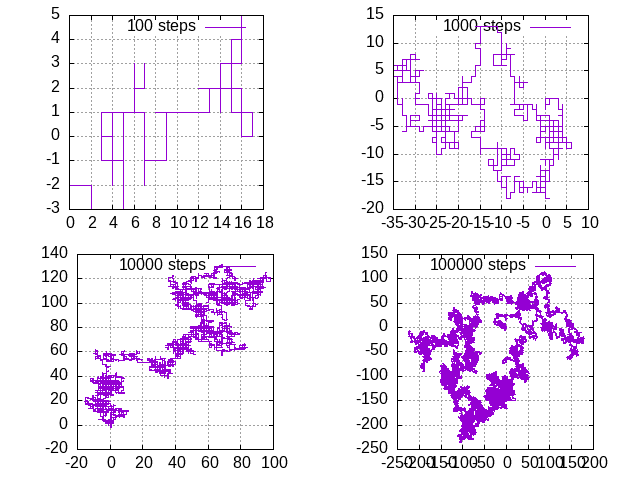
../_images/walk-path.png — Figure 12.11.1 The path walked by a drunkard for 100, 1000, 10000 and 100000 steps. Note that for long walks the figure starts looking like a *fractal*.

12.12. Matplotlib animation of a random walk

Using matplotlib we can animate rather smoothly in real time. Try this program in Listing 12.12.1:

Listing 12.12.1 walk_matplotlib.py

#! /usr/bin/env python3

"""This program plots an animated random walk using matplotlib.  You can run it with:

walk_matplotlib.py 500 1000

which would show 500 video frames to take 1000 steps.

A long run that shows how you can generate self-similar pictures could
be:

matplotlib.py 10000 100000

You could remove a zero from the first number to make it draw much faster.

"""

import sys
import math
import random

import matplotlib.pyplot as plt
import numpy as np

def main():
    n_frames = 500
    n_steps = 1000
    walk_file = 'walk_matplotlib.dat'
    if len(sys.argv) == 3:
        n_frames = int(sys.argv[1])
        n_steps = int(sys.argv[2])
    if n_frames > n_steps:
        raise Exception('*error* cannot have more frames than steps')
    x = 0
    y = 0
    take_walk(x, y, n_frames, n_steps)
    plt.waitforbuttonpress()


def take_walk(x, y, n_frames, n_steps):
    """Takes a random walk, plotting the trajectory as we go."""
    assert(n_frames <= n_steps)
    draw_interval = int(n_steps / n_frames)
    assert(draw_interval > 0)
    print('## draw_interval: ', draw_interval)
    # some boiler plate stuff to prepare the matplotlib drawing area
    xmax = max(x, 10)
    ymax = max(y, 10)
    xmin = min(x, -10)
    ymin = min(y, -10)
    fig = plt.figure()
    ax = plt.axes()
    ax.set_xlim(-10, 10)
    ax.set_ylim(-10, 10)
    plt.grid(True)
    step_list = []
    full_path_x = []
    full_path_y = []
    line, = ax.plot(full_path_x, full_path_y, color='g', linewidth=3.0)
    # now that the plotting layout and variables are ready, we can
    # start the iteration
    for i in range(n_steps):
        step_x = 0
        step_y = 0
        prev_x = x
        prev_y = y
        ## generate steps of -1 or +1 in x and y directions
        ## use a coin toss to decide if we go in the x or y direction
        if random.randint(0, 1) == 0:
            step_x = random.randint(0, 1) * 2 - 1
        else:
            step_y = random.randint(0, 1) * 2 - 1
        x = x + step_x
        y = y + step_y
        # readjust the limits to account for where we are now
        xmax = max(xmax, x, ymax, y, -xmin)
        ymax = max(ymax, y, xmax, x, -ymin)
        xmin = min(xmin, x, ymin, y, -xmax)
        ymin = min(ymin, y, xmin, x, -ymax)
        ax.set_xlim(xmin, xmax)
        ax.set_ylim(ymin, ymax)
        distance = math.sqrt(x*x + y*y) # distance from the origin
        if i < 1:
            continue   # don't plot the first step

        # our plotting approach will use the matplotlib
        # line.set_data() method, which uses a variable with all the
        # data in it.  this makes for smoother animation and better
        # memory use than other approaches, like drawing over previous
        # plots.
        full_path_x.append(x)
        full_path_y.append(y)
        prev_x = x
        prev_y = y
        # now do some clever balancing of how often we update the
        # drawing; this is based on the two input variables: the
        # number of frames and the number of steps.
        if i % draw_interval == 0:
            line.set_data(full_path_x, full_path_y)
            linewidth = 1 + 20.0 / (xmax - xmin)
            line.set_linewidth(linewidth)
            ax.figure.canvas.draw_idle()
            print(i, '   ', x, '   ', y, '   ', math.sqrt(x*x + y*y),
                  '   ', linewidth)
            plt.pause(0.000001)
    return step_list


main()

There are many things you might find notable in this program. The one I will comment on here is that there is a particular way in which we update the line in the plot (the key animation step).

Instead of using drawing commands to draw a new line, we use the line.set_data(). This is for speed: redrawing would be very slow, while updating the internal plot data will write to screen much faster.

Another thing to note is that in this example we don’t use matplotlib’s animation approach. We could probably change this program over, but it might be good to first see how to program it directly.

There is a tutorial on matplotlib animations here:

https://jakevdp.github.io/blog/2012/08/18/matplotlib-animation-tutorial/

archived at:

https://web.archive.org/web/20220601192231/https://jakevdp.github.io/blog/2012/08/18/matplotlib-animation-tutorial/

12.13. Making a movie from walk frames

12.13.1. Reviewing graphics and animation

In this session I will start with a discussion of graphical and video file formats: mention png (portable network graphics), jpeg (joint picture expert group), and mpeg (motion picture expert group).

We can use either ffmpeg or convert or mencoder to convert the sequence of frames into a movie.

In other mini courses, for example Section 32.1.3.1, we have used the same idea of generating several individual frames and then using ffmpeg to make a movie out of them. We can go to that section and try those examples, and then return here.

It basically boils down to this. Find an image to work with, for example a Hubble Space Telescope image of the Pillars of Creation in the Eagle nebula:

wget https://ia902307.us.archive.org/7/items/pillars-of-creation-2014-hst-wfc-3-uvis-full-res-denoised/Pillars_of_creation_2014_HST_WFC3-UVIS_full-res_denoised.jpg
# rename it something simpler
mv Pillars_of_creation_2014_HST_WFC3-UVIS_full-res_denoised.jpg pillars_of_creation_hubble_big.jpg
# make it smaller
convert -resize 1000x pillars_of_creation_hubble_big.jpg pillars_of_creation_hubble.jpg

Then, to experiment with making animations, try this sequence:

for i in `seq -w 0 360`
do
    echo "rotating by $i degrees"
    convert pillars_of_creation_hubble.jpg -rotate $i pillars_of_creation_hubble-rotate${i}.jpg
done

ffmpeg -framerate 20 -i pillars_of_creation_hubble-rotate%03d.jpg rotate-movie-fr20.mp4

Then you can view rotate-movie-fr20.mp4 with your favorite movie plyer.

12.13.2. Making individual frames of the random walk

We will use gnuplot to generate a sequence of images in png format.

Start with a file with a million lines of random walk output. You can do this as shown above with:

$ python3 walk.py 1000000 > walk-1000000.dat

gnuplot usually draws its output to the screen, but we can change that behavior and have it generate a .png file. To do so we add a couple of lines at the top:

$ gnuplot
# and at the gnuplot> prompt:
set grid
set size square
set terminal png
set output 'walk-100.png'
plot '<tail -100 walk-1000000.dat' using 2:3 with lines
set terminal png
set output 'walk-1000.png'
plot '<tail -1000 walk-1000000.dat' using 2:3 with lines
quit
# at the shell, possibly in another window, you can type:
$ ls

After running this last example you should find that there are a couple of new files in this directory: walk-100.png and walk-1000.png. If you view them with your favorite image viewer (you might want to consider the viewer geeqie) you will see that they are indeed the plots you wanted to make.

Our first task is to automate this process to generate hundreds or thousands of individual static images. The program walk_movie.py in Listing 12.13.1 does so.

Listing 12.13.1 walk_movie.py

#! /usr/bin/env python3

"""Makes a movie from a random walk output file."""

import os
import sys


def main():
    n_frames = 500
    n_steps = 1000000
    walk_file = 'walk-%d.dat' % n_steps
    if len(sys.argv) == 3:
        walk_file = sys.argv[1]
        n_frames = int(sys.argv[2])
        n_steps = int(os.popen("wc %s | awk '{print $1}'" % walk_file).read())
    print('Using %d frames from input file %s which has %d steps'
          % (n_frames, walk_file, n_steps))

    if not os.path.exists(walk_file):
        print('error: you must prepare the file %s -- you can do this with:'
              % walk_file)
        print('    ./walk.py %d > %s' % (n_steps, walk_file))
        sys.exit(1)

    gp_fname = 'walk_step.gp'
    for frame in range(0, n_frames):
        this_step = int(frame*n_steps/n_frames) # go in jumps
        this_step = max(this_step, 10)           # avoid small numbers
        png_fname = 'walk_frame-%06d.png' % frame
        if os.path.exists(png_fname):
            sys.stdout.write('## no need to rebuild %s        \r' % png_fname)
            sys.stdout.flush()
            continue
        gp = """set grid
set size square
set terminal png
set output '%s'
plot '<head -%d %s' using 2:3 with lines
quit\n""" % (png_fname, this_step, walk_file)
        f = open(gp_fname, 'w')
        f.write(gp)
        f.close()
        os.system('gnuplot %s' % gp_fname)
        percent = 100.0*frame / n_frames
        if frame % 10 == 0:
            sys.stdout.write('Making individual frames -- %.02f%% completed          \r' % percent)
            sys.stdout.flush()
    print()
    print('## now you can make a movie with something like:')
    print('ffmpeg -framerate 24 -i walk_frame-%06d.png walk-movie.mp4')
    print('## or:')
    print('ffmpeg -framerate 24 -i walk_frame-%06d.png walk-movie.ogg')
    print('## or:')
    print('convert walk_frame*.png walk-movie.mp4')
    print('## or for a more powerful encoder:')
    print('mencoder "mf://walk_frame*.png" -o walk-movie.mp4 -ovc lavc')
    print('## or in reverse:')
    print('ls -1 -r walk_frame*.png > reverse_filelist')
    print('mencoder "mf://@reverse_filelist" -o walk-movie-reverse.mp4 -ovc lavc')

main()

If you run this program it will generate n_frames different frames (the default in the program is 1000). To make a more satisfying movie we should increase this, but let us start with 1000 to make the program run more quickly.

walk_movie.py will pick out the random walk steps jumping 100 every time (see the line that says n_steps = i*100). It then generates a sequence of gnuplot commands like the one we saw above to generate file names that look something like walk_frame-000023.png.

If we run the program and the list the directory:

$ python3 walk_movie.py
$ ls

we see that the program has generated a bunch of walk_frame-*.png files (initially 1000 of them). Your favorite graphic viewer might allow you to press the space bar and almost see an animation of them.

Now let us talk about making a movie. There are several programs which encode a sequence of static image files into an mpeg movie. I mention three such programs: ffmpeg, convert and mencoder. The walk_movie.py program gave us a tip on how to run those programs to encode all the frames into the movie file walk-movie.mp4:

$ ffmpeg -framerate 24 -i walk_frame-%06d.png walk-movie.mp4

or

$ convert walk_frame*.png walk-movie.mp4

or

$ mencoder "mf://walk_frame*.png" -o walk-movie.mp4 -ovc lavc

or, to make a movie in reverse:

$ ffmpeg -framerate 24 -start_number -999999 -i walk_frame-%06d.png walk-movie.mp4
## FIXME: the reverse order with a negative start number needs to
## be ironed out.  Maybe ffmpeg can take an `ls -r ...` on the
command line.

or

$ ls -1 -r walk_frame*.png > reverse_filelist
$ mencoder "mf://@reverse_filelist" -o walk-movie-reverse.mp4 -ovc lavc

Note that the simplest and fastest approach is to use ffmpeg (the “Swiss army knife” of video and audio formats) so I will continue with ffmpeg for my examples.

You can now play these movies with your favorite movie player - I recommend vlc, though your system might come with totem already installed:

$ vlc walk-movie.mp4
$ vlc walk-movie-reverse.mp4

I wrote walk_movie.py to only generate 500 frames so that it can run quickly when I give examples or when I build this book, but you should increase that number a lot so you can see a longer movie with more detail.

Playing the movie shows you the growth of a fractal. It is interesting to watch how sometimes it adds paths in a clump, while sometimes it darts off into another sector of the plane, creating some filaments that connect the thicker bushes.

12.14. Discussion

Discuss the result of these experiments with your partners. Ask each other the following questions and write slides to present your answers. You might write one slide for each few related questions. You may include any of the plots you made in this course into your slides.

Look at the first two plots we made. In the first one (single coin flips) note that a new point in the plot is completely independent of the previous ones. In the second one (running average of single coin flips) is each new point on the plot related to previous ones? Are there two types of random events - those that are fresh and new, and those that add a small random change to a previous state? The former is called a Poisson process, the latter is called a Markov process or a Markov chain.
Look at the plot of averages from the single coin experiment and tell a story of what is going on in that plot, addressing the fact that initially it fluctuates quite a bit and later it seems to converge to 0.5.
Is this related to how many more ways you can create 10 disordered coins than 10 ordered coins?
Was it more work to restore the 10 coins to “heads up” or was it more work to toss them with the spatula.
Why it easier to restore 10 coins to their initial “heads up” state than to restore the drop of ink to its inital state?
Is it easier to go from order to disorder or from disorder to order?
Have you heard of Entropy? If not, now you have. Entropy is related to the idea of disorder. One of the deepest laws in physics is the Second Law of Thermodynamics. One of the ways of stating the second law is that the entropy of the universe is always increasing.
Referring back to the Emergent Behavior short course, remember how in that situation we examined systems that go from chaos to order: a random first row in a cellular automaton becomes a pattern of triangles, and a random initial state in John Conway’s game of life can produce ordered patterns as well as gliders. Discuss how emergent behavior seems to produce order out of chaos - does this violate the second law of thermodynamics?
Discuss the cycle that brings to living creatures: trees, flowers, cats, dogs, horses, humans… Is each living creature more or less ordered than the molecules in the earth and air from which that creature is made?