22. Optimal Stopping
Section author: Malcolm Smith <msmith.malcolmsmith@gmail.com>
[status: first draft]
22.1. Motivation, Prerequisites, and Plan
Motivation
When you are confronted with a decision involving incomplete information, it can feel very daunting and stressful. Unfortunately, almost every decision you make in your life will be made with some level of incompleteness in your information. This can come in many forms, such as deciding where to park, or the more serious example of when to settle down with a romantic partner. Fortunately, there are rules you can follow to help you make the best decisions possible! These come from an area of mathematics known as optimal stopping, which, as the name implies, can tell you when it is optimal to stop.
Prerequisites
The 10-hour “Serious Programming” course.
The “Data and First Plots mini-course in Starting out - data files and first plots.
Plan
This course is intended to be a lighthearted one, and won’t go into the more mathy side of optimal stopping. That being said, we will first look at a generic example like the Employee Problem, arguably the most famous example of optimal stopping, and several of its variations. We will then move onto more realistic scenarios, including the example of trying to find a parking spot in a crowded city.
22.2. What is Optimal Stopping?
Optimal stopping is the science of deciding when to stop. This is an interesting concept, because you have to condense a lot of information into a single, binary decision: keep going, or stop? This can actually be quite a complex process, especially as the number of variables you have access to increases. For the sake of simplicity, we are going to assume that there is only one variable you care about (how well a job candidate will do, how satisfied you are with a romantic partner, etc.). These may seem like they are impossible to quantify, and they are, which is why this theory is often used in fields like economics or medicine where you do have exact numbers. Our models will be entirely numeric, so you could really call most of these example a lot of other things, especially because we will be using a random number generator to generate the scores we are interested in. With that background, let us look at the specific methods we will be using.
The basic principle we will employ is a look-before-you-leap model. What this means is that we will spend some portion of the time (or some portion of the options) simply looking, without taking anything we see. Then, after our looking period is over, we employ some other rules based on what we saw during the looking period to decide when to stop. For example, a simple rule that we will be using at some point is simply to select the first option after the looking period that is better than anything we saw during the looking period. This method is not without its flaws; if you happen to get the absolute best option during the looking period, you will be stuck with the last option, because nothing will have been up to the standard that the best option set. However, it is still a fairly interesting model, and we will examine it in time.
Before moving on to the implementation sections, a word about overall method is required. We will be using what is more or less a trial-and-error approach to this, known fancily as a Monte Carlo algorithm. This stems from a method for determining the area of some 2D shape: put the shape inside a square, then shoot a bunch of little BBs (or other small objects) at the square, and count how many hit the shape. If you do this with enough BBs that are small enough, you will eventually get a very good approximation of the area. This method is shown quite nicely in Figure 22.2.1.
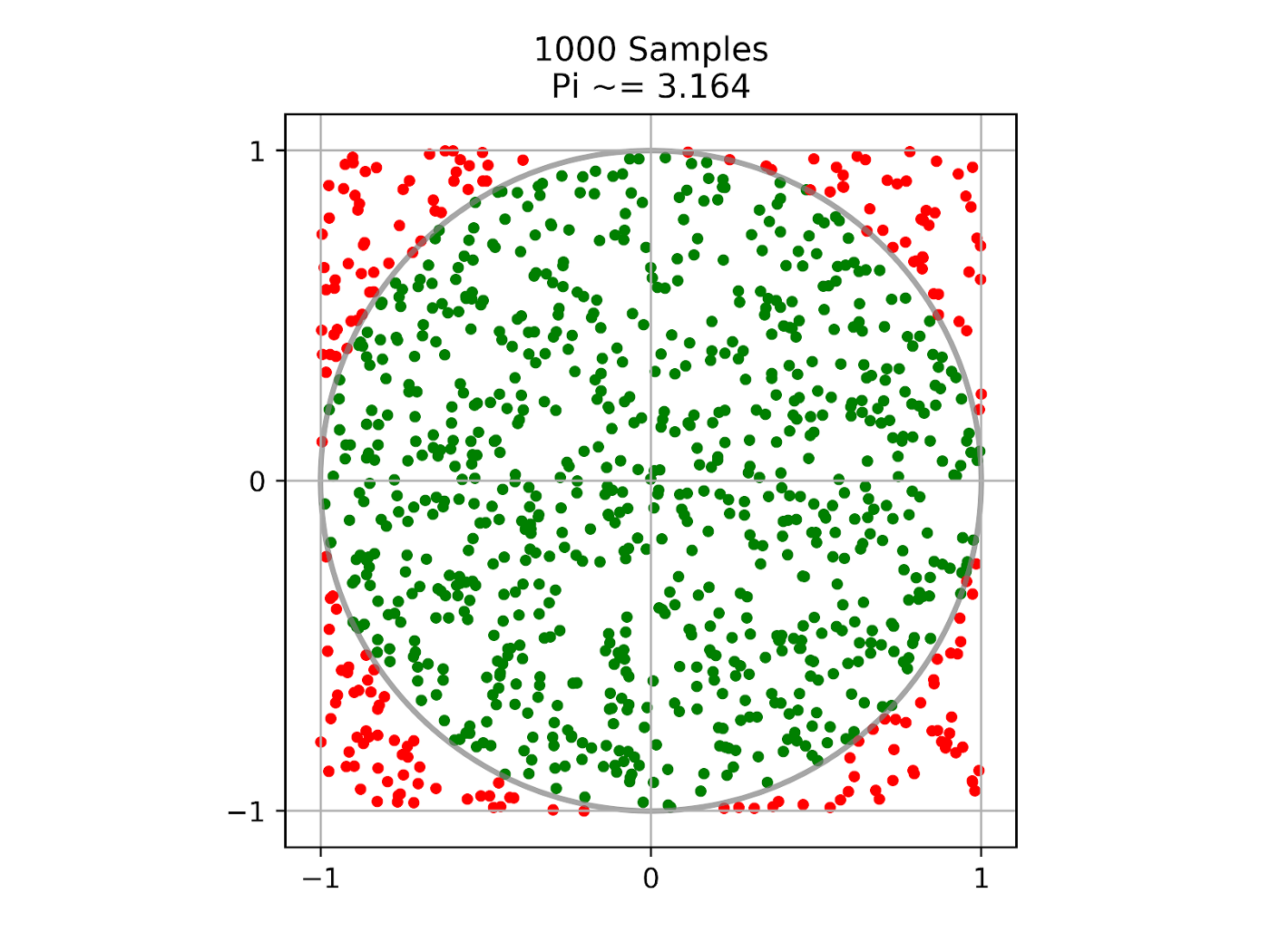
Figure 22.2.1 An image demonstrating the monte carlo method for estimating pi.
And yet, this feels like cheating somehow. Yes, we did find the area, but wasn’t there… a nicer way to do this? This analogy is not perfect to what we will be doing, but the brute force approach is the same. There is a large amount of theory that goes into optimal stopping, and we will entirely ignore it, discovering the best setups through brute force. If you want to learn the theory, there are some great article linked in the Further Reading section at the bottom, though be warned they have quite a bit of heavy jargon and math.
22.3. The Employee Problem
The setup for the employee problem is this: you, a recently promoted manager, are in need of an employee. There is very large supply and demand for them right now, meaning a somewhat absurd 100 people have applied for the position. You are the only person capable of deciding who would make a good employee for you, so you must interview each one personally to decide how good they are. However, because demand for secretaries is so high, you cannot come back to someone you have already interview. You must make the decision about hiring someone right after the interview. Assume that your goal is simply to find the absolute best employee, and all the others are equal in your eyes. Also assume that if you interviewed every one of them, you could rank them precisely from best to worst. With all of that in mind, what would be your algorithm for deciding when to stop looking and hire someone?
As mentioned in the motivation section, this can be a daunting task. You don’t know how good the people you haven’t interviewed yet are, so what if you stop to early and hire someone who isn’t the best? Conversely, what if you are too cautious and end up missing the best candidate and have to settle for less? Finding the right person will thus have to be the result of a compromise between the two. As we said in the previous section, the type of algorithm we are using is called “look before you leap”, or simply “look and then leap”. Because the list of people always advances, the only decision out algorithm will have to make is when to move from the look phase to the leap phase.
To find this, we will use the following algorithm:
Choose some stopping point along the list of candidates
Up until that point, hire no one; merely keep track of the highest scoring candidate
After that point, hire the first person you see who is better than anyone in the first phase.
If no one meets the bar, hire the last person you interview.
This strategy, with the right stopping point, is the best method for finding the best candidate, with a percentage chance that this program will be able to tell us:
import sys
import random
import matplotlib.pyplot as plt
def main():
stopping_bounds = [0.15, 0.5] # bounds for stopping point
n_candidates = 100
n_trials = 10000
lower_stop = round(stopping_bounds[0] * n_candidates)
upper_stop = round(stopping_bounds[1] * n_candidates)
max_chance_best_found = 0
best_stop = 0
chances_best_found = []
for stop in range(lower_stop, upper_stop):
chance_best_found = find_chance_best_found(stop, n_candidates, n_trials)
chances_best_found.append(chance_best_found)
if chance_best_found > max_chance_best_found:
max_chance_best_found = chance_best_found
best_stop = stop
print(f'Best stopping point was after candidate {best_stop}, with a '
f'{round(max_chance_best_found * 100, 4)}% chance of finding '
f'the best candidate')
fig, ax = plt.subplots()
ax.set_xlabel('Stopped after candidate')
ax.set_ylabel('Chance best found')
ax.scatter(range(lower_stop, upper_stop), chances_best_found)
fig.savefig('employee-problem.png')
fig.savefig('employee-problem.svg')
fig.savefig('employee-problem.pdf')
print('Saved file to employee-problem.png, .svg, and .pdf')
if not (len(sys.argv) > 1 and sys.argv[1] == '--non-interactive'):
plt.show()
def find_chance_best_found(stop, n_items, n_trials):
"""returns the chance of finding the best candidate when stopping
looking at a given stopping point"""
chance_best_found = 0
for trial in range(n_trials):
items = list(range(n_items))
random.shuffle(items)
bar = 0 # bar is the lowest you would accept after the looking period
for i in range(stop):
if items[i] > bar:
bar = items[i]
# if no further candidates hit the bar, you're stuck with the
# last one
selection = items[-1]
for i in range(stop, n_items):
if items[i] > bar:
selection = items[i]
break
if selection == n_items - 1:
chance_best_found += 1 / n_trials
return chance_best_found
main()
When run, this should produce something like Figure 22.3.1:
Figure 22.3.1 A graph comparing stopping point to the chance of selecting the best candidate.
To keep the running time to a reasonable level, we limited the program to 10000 trials per stopping point, which will result in some variance in the answer. However, after running it a couple times, you should notice that the best stopping point tends to be around 37, and so does the percent chance of finding the best candidate at that point. This is not a coincidence, nor is it specific to 100 candidates. Generally speaking, the best stopping place is around 36.8% of the way through the candidates, and the accuracy when stopping there is also going to be 36.8%. For those of you with a math background, this number may look familiar: it’s \(\frac{1}{e}\), where \(e \approx 2.7182\) is Euler’s number and the base for natural logarithms. The reason for this involves a complicated derivation, which we will not get into here, but for those who are interested the wikipedia page on the problem can be found here.
This is interesting, but it’s still only scratching the surface of optimal stopping. There are many variations on this problem, though the two we will focus on for the rest of the chapter are a) what if we don’t need the very best, and b) what if we have some chance of being able to hire an applicant after the interview is over?
To address the first question, we need more processing power. The reason for this is that as we broaden out search to include the top two candidates, we need three phases of interviews. The first and second are the same, but the third is when we would hire anyone who is better than the second best candidate in the looking phase. This means we have 2 stopping places, so the search will take a much greater time. Of course, we may not reach the third phase, but we still have to define the second stopping place. With that in mind, let us alter and then run the program above:
import sys
import random
import matplotlib.pyplot as plt
def main():
first_stopping_bounds = [0, 1] # bounds for stopping point
second_stopping_bounds = [0, 1]
n_candidates = 100
n_trials = 10000
lower_first_stop = round(first_stopping_bounds[0] * n_candidates)
upper_first_stop = round(first_stopping_bounds[1] * n_candidates)
lower_second_stop = round(second_stopping_bounds[0] * n_candidates)
upper_second_stop = round(second_stopping_bounds[1] * n_candidates)
max_chance_best_found = 0
chances_best_found = []
for first_stop in range(lower_first_stop, upper_first_stop):
# order best found chances by both stopping points
chances_best_found.append([])
for second_stop in range(lower_second_stop, upper_second_stop):
if second_stop <= first_stop:
chances_best_found[-1].append(0)
continue
else:
chance_best_found = find_chance_best_found(first_stop,
second_stop,
n_candidates,
n_trials)
chances_best_found[-1].append(chance_best_found)
if chance_best_found > max_chance_best_found:
max_chance_best_found = chance_best_found
best_first_stop = first_stop
best_second_stop = second_stop
print(f'Tried stopping points {first_stop} and {second_stop}, '
f'resulting in a chance of {chance_best_found}.')
print(f'Best stopping points were after candidates {best_first_stop} and '
f'{best_second_stop}, with a {round(max_chance_best_found * 100, 4)}%'
f' chance of finding one of the five best candidates')
ys = []
for i in range(len(chances_best_found)):
ys.append(chances_best_found[i][best_second_stop - lower_second_stop])
fig, ax = plt.subplots()
ax.set_xlabel('Stopped after candidate')
ax.set_ylabel('Chance top two found')
ax.scatter(range(lower_first_stop, upper_first_stop), ys)
ax.scatter(range(lower_second_stop, upper_second_stop),
chances_best_found[best_first_stop - lower_first_stop])
fig.savefig('find-top-two.png')
fig.savefig('find-top-two.svg')
fig.savefig('find-top-two.pdf')
print('Saved file to find-top-two.png, .svg, and .pdf')
if not (len(sys.argv) > 1 and sys.argv[1] == '--non-interactive'):
plt.show()
def find_chance_best_found(first_stop, second_stop, n_items, n_trials):
"""returns the chance of finding the best item when stopping
looking at given stopping points"""
chance_best_found = 0
for trial in range(n_trials):
items = list(range(n_items))
random.shuffle(items)
bar = 0 # bar is the lowest you would accept after the looking period
second_bar = 0
for i in range(first_stop):
if items[i] > bar:
second_bar = bar
bar = items[i]
# if no further candidates hit the bar, you're stuck with the last one
selection = items[-1]
for i in range(first_stop, second_stop):
if items[i] > bar:
selection = items[i]
break
if items[i] > second_bar:
second_bar = items[i]
for i in range(second_stop, n_items):
if items[i] > second_bar:
selection = items[i]
break
if selection >= n_items - 2:
chance_best_found += 1 / n_trials
return chance_best_found
main()
Figure 22.3.2 The result of the above program. The blue dots are the first stopping place, the orange are the second.
After running this, it should become clear why we have limited ourselves to the top two. Every rank lower you are willing to go, the program take exponentially longer to run. In fact, it is probably advisable to turn down the number of candidates or the number of trials, because it will take a very long time to run with the current parameters. The other striking thing is that the orange dots actually are highest when the second stopping point is 99, meaning the optimal strategy is to never go to the third phase at all. This is likely due to the fact that there’s a fairly high chance that selecting the first thing you find that’s higher than the second best example in the looking phase simply leaves too much chance that you will select something below the top two. In an effort to marginally increase the chances, we actually added a much bigger detrimental factor, and the program automatically discovered it and filtered it out.
While we are not going to have a program that runs for for than three phases, we can make the target range for the selected candidate wider. This will make the chances of error in the third zone lower, meaning it will actually be utilized. What is the narrowest range that hits this threshold? (Hint: change the number in the last if statement.)
Moving on to yet another flavor of the employee problem (this is the last one, I promise), we will now consider something else that is likely to be true in the real world: you can go back to a previous candidate, but they may have already moved on. This is a fairly major change, and it should have a significant impact on the optimal stopping point for the looking phase (this example is back to just two phases). A detail to note is that we will be decreasing the chance of a candidate still being interested the longer ago their interview was, which makes sense in most real-world contexts. Implementing these changes really only takes a couple extra lines of code:
...
n_trials = 10000
call_back_chance = 0.5
...
for stop in range(lower_stop, upper_stop):
chance_best_found = find_chance_best_found(stop, n_candidates, n_trials, call_back_chance)
chances_best_found.append(chance_best_found)
...
def find_chance_best_found(stop, n_items, n_trials, call_back_chance):
"""returns the chance ... """
...
break
for i in reversed(range(selection, n_items)):
if random.random() < call_back_chance * (1 - items.index(i)/100):
selection = i
break
if selection == n_items - 1:
...
Note that these are changes to the first employee problem program, not the more recent one. When you run the program as is, it will produce a graph (shown in Figure 22.3.3) that looks very similar to the one produced for an example with no calling candidates back. This is because the possibility of passing over the best candidate in the looking phase is to some extent nullified by the ability to call them back later, but only to a point: if they don’t accept your new offer (and the chance of that is high, because of their early position in the queue), you are going to be stuck with an inferior candidate. However, there is some small chance that this gamble will pay off, and that can be seen in the fact that the maximum is more closely centered around 40-41 that 37 as it was previously.
Figure 22.3.3 A plot shown the small impact of the ability to call back.
This may seem a bit underwhelming at first, but where this program can really shine is if we broaden a “success” to include more than just the top candidate. We are otherwise leaving the program untouched, we simply change the line
if selection == n_items - 1:
to
if selection >= n_items - 2:
You can do the same in the original employee problem function, and the difference should become clearer upon running these update versions of the programs. When shown side by side, there is a stark difference:
Before learning which of these is which, try to figure it out for yourself: the numbers on the y-axis should be a clue, as should the fact that one is skewed further to the left. The figure on the left was created with the original algorithm, while the one of the right was create with the one that simulates calling back. This can be seen in the chance of success (25% higher in the right one, in line with the 50% call back success chance), as well as the fact that the peak is further to the left, the reason for which we discussed earlier. Feel free to play around with how many candidates away from the best is a “success”, and you should see an even bigger gap emerge between the two.
22.4. A (marginally) More Useful Application: Parking
To use optimal stopping in a scenario where you are looking for a place to park, we need a new problem definition, and new methods. The first is arguably simpler (and required for the second), so let us start there. To make our model as simple as possible, we will assume that you are driving down a one-way street with parking down one side of the street. Your destination is at the end of the street, and your goal is to walk as little as possible (likely not the healthiest, but oh well). Also, for simplicity’s sake, we will not allow block-circling in our model, and simply make you walk a very far distance if you reach the end of the block without finding a spot. To maintain consistency with the previous problems, there will be 100 parking spots, some number of which will be filled. This brings us to the final parameter within our control: the occupancy rate, or the chance that a given parking spot is taken. This will apply equally across all parking spots, even the most desirable ones. Finally, we need a way to measure success: in the previous examples, we used a simple binary “did you find the best candidate?”, which is insufficient in complexity for this case. What we can try instead is an average distance walked at a given stopping point. In this case, a stopping point refers to where you start looking for a spot; when you see one beyond this point, you take it. Another assumption you may have noticed is that you cannot scan the parking spots ahead; this is for ease of modeling, but it could also be due to a very rapid turnover of parking spots.
With the laborious problem statement out of the way, let us start coding a solver. To do this, we need a main function, which is very similar to the previous main function:
def main():
stopping_bounds = [0, 1] # bounds for stopping point
n_spots = 100
n_spots_taken = 90
n_trials = 10000
lower_stop = round(stopping_bounds[0] * n_spots)
upper_stop = round(stopping_bounds[1] * n_spots)
min_avg_walking_distance = n_spots + 1 # a number guaranteed to be greater than the greatest possible walking distance
avg_walking_distances = []
best_stop = -1 # assign arbitrary value
for stop in range(lower_stop, upper_stop):
avg_walking_distance = find_avg_walking_distance(stop, n_spots, n_spots_taken, n_trials)
avg_walking_distances.append(avg_walking_distance)
if avg_walking_distance < min_avg_walking_distance:
min_avg_walking_distance = avg_walking_distance
best_stop = stop
print(f'Tried stopping after spot {stop}, resulting in a walking distance of {avg_walking_distance}.')
print(f'Best stopping place was {best_stop}, with an average walking distance of {min_avg_walking_distance}.')
plt.scatter(range(lower_stop, upper_stop), avg_walking_distances)
plt.show()
As you can see, this is almost (but not quite) identical to the main function in the original employee problem solving algorithm. The real differences will be in the other function:
def find_avg_walking_distance(stop, n_spots, n_spots_taken, n_trials):
"""returns how far you would have to walk given the parameters"""
total_walking_distance = 0
for i in range(n_trials):
spots = list(range(n_spots))
random.shuffle(spots)
taken_spots = spots[:n_spots_taken]
spots.sort()
look_spots = spots[:stop]
available_look_spots = [i for i in look_spots if i not in taken_spots]
available_look_spots.append(n_spots + 1) # penalty for not finding a spot
total_walking_distance += available_look_spots[0]
return total_walking_distance / n_trials
Putting this all together (along with importing random and matplotlib, and a main call at the bottom) should produce an image like Figure 22.4.1:
Figure 22.4.1 A graph illustrating the best way to park.
This graph is not particularly surprising, saying walking distance is minimized when you start looking to park about 22 spots away, or 3 blocks. This is somewhat intuitive, because 3 blocks is a reasonable distance to look for parking in when it is not particularly busy (90 out of 100 spots being taken is very open). However, when we increase the amount of spots taken just a little, to 97, something unexpected happens.
Figure 22.4.2 A graph showing the perils of parking in a busy area.
As you can see, despite the relatively modest increase in taken spots (7% of the total), the best place to start looking is now twice as far as way! And after a moments’ thought, something even more surprising may occur to you. At 99 spots taken, it will obviously be best to start as far back as possible, because that maximizes your chances of finding the one parking spot… which requires doubling the search distance again, this time with a 2% increase in parking density. This is a clear sign of exponential growth, which also explains why parking in a busy place is so frustrating: it literally takes orders of magnitude longer when its even a little busier. This is obviously something civil engineers and city planners do not want, as discussed in the Further Reading section.
22.5. Conclusion
In this chapter, we discussed various aspects of optimal stopping theory through a Monte Carlo approach. This means we attempted to loosely model the situations, rather than relying on theory. The Monte Carlo method is incredibly useful for being able to solve problems before the theory around them is understood, which can often drive the theory forward. Regardless, having an understanding of them and some of their applications is very useful for anyone, but especially those who want to use a computer to solve problems.
We implemented three flavors of the employee problem, which deals with a hiring decision under imperfect information. Here, we found one of those mathematical constants pop up out of nowhere: the solution to the basic version of the employee problem, as it turned out, had e in it twice. After tweaking the model some to make it a little more realistic, we moved on to a much more practical real-life example: parking. We saw not only how to best park under certain conditions, but also why parking in crowded areas is so frustrating.
Hopefully this chapter deepened your understanding of the Monte Carlo method and optimal stopping, or introduced you to them. Going forward, I would encourage you to think about all the “stopping points” you set in life, and think of there could be a way to model it. It is always interesting to see real world applications of examples like these, and this particular case is rife with opportunity.
22.6. Further Reading
Basic introduction to the concept: https://towardsdatascience.com/when-should-you-stop-searching-a439f5c5b954
Game theory take on optimal stopping: https://slideplayer.com/slide/9266138/
Civil engineer talks about parking density: https://medium.com/galleys/optimal-stopping-45c54da6d8d0