4. More taylor series

4.1. Exponentials

4.1.1. The number \(e\): base for natural exponentials and logarithms

In earlier lessons we discussed the exponential function at length. Here we discuss some of the reasons for which we consider Euler’s number \(e\) to be the “natural” base for exponentials and logarithms, analogously to how radians are the natural unit of measure for circles.

Part of this is a visual exploration of \(e^x\) and an graphical look at its slope, to then conclude that:

\[\frac{d e^x}{dx} = e^x\]

which is not true for other bases, like \(2^x\) and \(10^x\)

We can also mention that:

\[e = \lim_{n \rightarrow \infty} \left(1 + \frac{1}{n}\right)^n\]

and calculate it for values of n like 1, 10, 100, 1000, 10000, … We can also calculate \(e\) with:

\[e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} + \dots = \sum_{k=0}^{\infty} \frac{1}{k!} \approx 2.71828182846\]

but the justification for that will only come when we show how to calculate the Taylor series for \(e^x\).

Caution

It is also worth mentioning that difference communities in math, science, and engineering use \(\log(x)\) to mean the natural logarithm (base \(e\)). Other communities will use \(\log(x)\) to mean the base 10 logarithm, and they say \(\ln(x)\) for the natural logarithm. I use the former approach, and the various programming language libraries (C, Python, …) do the same.

But we take a break from these notes as we get to use a proper text book to explore exponentials and logarithms in more detail.

4.1.2. The Taylor series for \(e^x\) – visually

First we look at it visually. We will want to plot terms in the following way in gnuplot and geogebra and desmos:

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
reset
set grid
set xrange [-1:3]
set terminal qt linewidth 3
plot exp(x) lw 2
replot 1
replot 1 + x
replot 1 + x + x**2 / 2!
replot 1 + x + x**2 / 2! + x**3 / 3!
replot 1 + x + x**2 / 2! + x**3 / 3! + x**4 / 4!
replot 1 + x + x**2 / 2! + x**3 / 3! + x**4 / 4! + x**5 / 5!
replot 1 + x + x**2 / 2! + x**3 / 3! + x**4 / 4! + x**5 / 5! + x**6 / 6!

In geogebra or desmos:

e^x
1
+ x
+ x + x**2 / 2!
+ x + x**2 / 2! + x**3 / 3!
+ x + x**2 / 2! + x**3 / 3! + x**4 / 4!
+ x + x**2 / 2! + x**3 / 3! + x**4 / 4! + x**5 / 5!
+ x + x**2 / 2! + x**3 / 3! + x**4 / 4! + x**5 / 5! + x**6 / 6!

4.1.3. The Taylor series for \(e^x\) – calculating the coefficients

Remembering that \(\frac{de^x}{dx} = e^x\) we can calculate:

\[\frac{d^k e^x}{dx^k} \bigg \rvert_{x = 0} = e^0 = 1\]

which gives us Taylor coefficients \(a_k = \frac{1}{k!}\) and the series looks like:

\[e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}\]

4.2. Miscellaneous Taylor expansions

Logarithms:

\[\begin{split}log(1 - x) = -\sum_{k=1}^{\infty} \frac{x^k}{k} \\ log(1 + x) = \sum_{k=1}^{\infty} (-1)^{k+1} \frac{x^k}{k}\end{split}\]

the first when \(|x| < 1\), the second when \(-1 < x \leq 1\)

Note that when you plot these logarithmic functions you will need to double check that your plotting program uses \(log()\) for natural logarithms. Some plotting programs use \(\ln()\) for natural logarithms.

Geometric series:

\begin{eqnarray} \frac{1}{1-x} = & \sum_{k=0}^{\infty} & x^k \\ \frac{1}{(1-x)^2} = & \sum_{k=1}^{\infty} & k x^{k-1} \\ \frac{1}{(1-x)^3} = & \sum_{k=2}^{\infty} & \frac{(k-1)k}{2} x^{k-2} \end{eqnarray}

when \(|x| < 1\)

4.3. Some square root expansions

Square root functions can get complicated. For example, the relativistic formula for the rest plus kinetic energy of an object with mass \(m_0\) is

\[E_{\rm total} = \frac{m_0 c^2}{\sqrt{1 - \frac{v^2}{c^2}}}\]

This has the famous Lorenz gamma factor:

\[\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]

We sometimes use a shorthand \(\beta = v/c\), where \(\beta\) is the velocity expressed as a fraction of the speed of light, and get:

\[\gamma = \frac{1}{\sqrt{1 - \beta^2}}\]

The first few terms in the taylor series expansion in \(\beta\) are (see the Cupcake Physics link in the resources chapter for details):

\begin{eqnarray} \gamma \;\; = \; & 1 + \frac{1}{2}\beta^2 + \frac{3}{8}\beta^4 + \frac{5}{16}\beta^6 + \frac{35}{128}\beta^8 \dots\\ = \; & 1 + \frac{1}{2}\frac{v^2}{c^2} + \frac{3}{8}\frac{v^4}{c^4} + \frac{5}{16}\frac{v^6}{c^6} + & \frac{35}{128}\frac{v^8}{c^8}\dots \end{eqnarray}

Putting this back into the formula for energy we get:

\[E_\textrm{total} = \; \frac{m_0 c^2}{\sqrt{1 - \frac{v^2}{c^2}}} = \; m_0 c^2 + \frac{1}{2} m_0 v^2 + \dots\]

For low values of \(v^2/c^2\) (i.e. \(v\) much slower than the speed of light) we have:

\[E_{\rm total} = m_0 c^2 + \frac{1}{2} m_0 v^2 + \dots\]

We can read off the terms and realize that the total energy is equal to the famous rest mass \(E_{\rm rest} = m_0 c^2\) plus the kinetic energy \(\frac{1}{2} m_0 v^2 + \dots\):

\[E_{\rm total} = E_{\rm rest} + E_{\rm kinetic} = m_0 c^2 + \frac{1}{2} m_0 v^2 + \frac{3}{8} m_0 \frac{v^4}{c^2} \dots\]

Let us explore the Lorenz gamma factor for values of \(v\) in the whole range from 0 to \(c\):

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
reset
set grid
set ylabel '\gamma'
set xlabel '\beta (v/c)'
set xrange [0:1]
set terminal qt linewidth 3
plot 1 / sqrt(1 - x**2)

Or in a web-based graphing calculator:

1 / (1 - x^2)^(1/2)

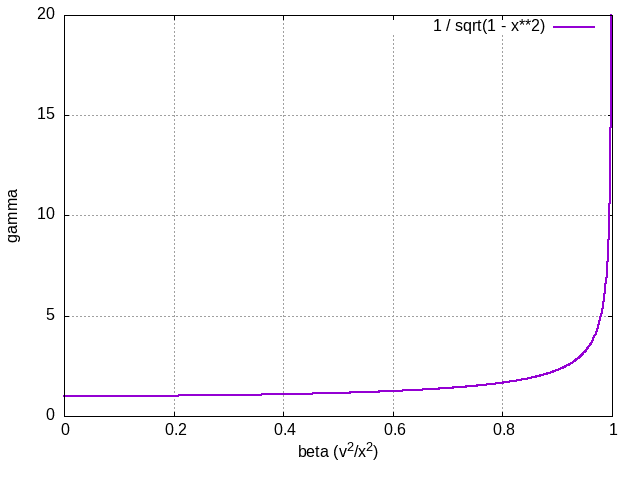
../_images/lorenz_factor.png — Figure 4.3.1 The lorenz factor as a function of \(\beta = v/c\). Note how it is close to 1 for most of the run, but grows out of control when \(v\) approaches the speed of light \(c\).

What insight does this give us on the energy of an object as it approaches the speed of light? Note that the formulae for length and time are:

\[\begin{split}L = \frac{1}{\gamma} L_0 \\ \Delta t' = \gamma \Delta t\end{split}\]

so the behavior of \(\gamma\) as a function of \(\beta\) (and thus \(v\)) also affects length and time.

Now let us look at the polynomial approximates in \(\beta\):

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
reset
set grid
set ylabel '\gamma'
set xlabel '\beta (v^2/c^2)'
set xrange [0:0.0001]
set terminal qt linewidth 3
plot 1 / (1 - x**2)
replot 1
replot 1 + (1.0/2) * x**2
replot 1 + (1.0/2) * x**2 + (3.0/8) * x**4
replot 1 + (1.0/2) * x**2 + (3.0/8) * x**4 + (5.0/16) * x**6