12. Approximating functions with series

As I mentioned in the “motivation” section Section 11, apprimationg by series is a technique used almost daily by scientists. Let us dive in.

12.1. Sequences and sums

The classic definition of sequences and sums should be familiar.

For our purposes a sequence is an ordered list of numbers. We can index it with an integer. We can describe these sequences any way we want, for example in English we could say the sequence of all positive integers or the sequence of all positive odd numbers or even numbers and so forth.

Or we can describe them with examples of numbers where you can spot the pattern, or with math operations that map from integers to the numbers in our sequence. We often use curly braces to show that an index like \(i\) or \(k\) should be understood to cover all integers (or non-negative or positive integers). For example:

\[ \begin{align}\begin{aligned}\textrm{Natural numbers}: \{i\}: 1, 2, 3, 4, 5, \dots\\\textrm{Even numbers}: \{2i\}: 2, 4, 6, 8, 10, \dots\\\textrm{Odd numbers}: \{2i - 1\}: 1, 3, 5, 7, 9, \dots\end{aligned}\end{align} \]

The sum of a sequence is simply the addition of all numbers in that sequence. We use the classice uppercase \(\Sigma\) notation. For example:

\[\sum_{k=1}^{100} k = 1 + 2 + 3 + 4 + \dots + 100\]

In this notation the famous Gauss summation formula is:

\[\sum_{k=1}^{N} k = 1 + 2 + 3 + 4 + \dots + N = \frac{N (N+1)}{2}\]

An example of a function defined by a sum is the Riemann zeta function, defined as:

\[\zeta(s) = \sum_{k=1}^{\infty} \frac{1}{k^s}\]

We are not really going to study the Riemann zeta function here, but we are interested in one value, \(\zeta(2)\):

\[\zeta(2) = \sum_{k=1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6}\]

This will give us an interesting playground to experiment with calculating values of \(\pi\).

Notice that a sum can be a finite sum or it can be a series: a sum of infinite terms where they get smaller and smaller so that the sum converges.

12.2. Do sums converge?

Convergence of series is a beautiful mathematical topic, but we will stick to our practical mode of operation here and mostly look at some examples to develop an intuition about it.

For example, the harmonic series diverges:

\[\sum_{k=1}^{\infty} \frac{1}{k}\]

which is interesting: it means that even though each number \(1/k\) is getting smaller and smaller, eventually tending to zero, the sum keeps growing without bounds.

Exercise: write a brief Python program which shows that if you pick any number, you can pick a number of terms of the harmonic series that gets bigger than that. Try it for a thousand, a million, then a billion, and see how many terms of the harmonic series you need to get bigger than that.

On the other hand, the alternating harmonic series:

\[\sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} \dots = \log(2)\]

converges to the natural logarithm of 2. A variant of the alternating harmonic series with just the odd terms is called the Leibniz series:

\[\sum_{k=0}^{\infty} \frac{(-1)^k}{2k+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} \dots = \frac{\pi}{4}\]

---

12.3. Approximating pi with series

Calculate an approximation to \(\pi\) using the Leibniz series:

import math
sum = 0
N = 16
for i in range(0, N+1):
    term = (-1.0)**i / (2*i+1)
    sum += term
    pi_approx = 4.0 * sum
    print(i, '   ', term, '   ', sum, '   ', pi_approx)

And with the Riemann zeta function:

import math
sum = 0
N = 16
for i in range(1, N+1):
    term = 1.0 / (i*i)
    sum += term
    pi_approx = math.sqrt(6.0 * sum)
    print(i, '   ', term, '   ', sum, '   ', pi_approx)

12.4. A digression on the factorial

\[\begin{split}0! &= 1\\ 1! &= 1\\ 2! &= 2\times1\\ 3! &= 3\times2\times1 = 3\times2!\\ 4! &= 4\times3\times2\times1 = 4\times3!\\ 5! &= 5\times4\times3\times2\times1 = 5\times4!\\ \dots\\ n! &= n \times (n-1)!\end{split}\]

There is a function for real numbers called the gamma function which has the same value as the factorial (of one less) when it hits the nonnegative integers:

\[\Gamma(n) = (n-1)!\]

The full definition of the gamma function for all real (and in fact complex) numbers is more advanced. I show it here, but it is a subject for much later on:

\[\Gamma(z) = \int_0^\infty x^{z-1} e^{-x} dx\]

How fast does the factorial grow? Linear? Polynomial? Exponential? Something else?

We can study that question a bit with the following:

specific values

First in your head, then using a calculator, calculate 0!, 1!, 2!, 3!, …, 10!

the function

Then use the following plot commands to see the gamma function:

$ gnuplot
# then at the gnuplot> prompt:
set grid
set xrange [0:2]
plot gamma(1+x)    # this is equivalent to x! for integers
replot x**2
replot x**5
replot 2**x
replot exp(x)
# pause and examine
set xrange [0:3]
replot
# pause and examine
set xrange [0:4]
replot
# pause and examine
set xrange [0:5]
replot
# pause and examine
set xrange [0:6]
replot
# pause and examine
set xrange [0:7]
replot
# pause and examine
set xrange [0:8]
replot
# pause and examine
set xrange [0:9]
replot

Once you have tried to pit \(n!\) (or \(\Gamma(n+1)\)) against various exponential functions, take a look at Stirling’s approximation to the factorial:

\[n! \approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n\]

which is just the first term of a more elaborate series:

\[n! \approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \left( 1 + \frac{1}{12 n} + \frac{1}{288 n^2} - \frac{139}{51840 n^3} - \frac{571}{2488320 n^4} + \dots \right)\]

Stirling’s formula is often used to calculate logarithms of \(n!\) like this:

\[\log n! = n \log n - n + O(\log n)\]

Looking closely at these formulae shows us that \(n!\) is indeed “super-exponential” in how it grows for large values of \(n\).

12.5. Experiments with series for sin and cos

We will start by doing experiments with the polynomials that give us approximations to \(\sin(x)\) and \(\cos(x)\).

12.5.1. Getting comfortable with radians

Remember: if a sensible angle feels like it’s in the range of 30 or 45 of 88 then it’s probably in degrees. If it’s expressed as \(\pi/4\), or some other multiple or fraction of \(\pi\), or a number that’s between 0 and 7, then there’s a good chance it’s measured in radians.

The conversion factor is \(\frac{\pi}{180}\) or its inverse \(\frac{180}{\pi}\):

\[ \begin{align}\begin{aligned}\textrm{angle_radians} = \textrm{angle_degrees} \times \frac{\pi}{180}\\\textrm{angle_degrees} = \textrm{angle_radians} \times \frac{180}{\pi}\end{aligned}\end{align} \]

You should get comfortable with the everyday angles we use and what they are in radians: 90deg = pi/2, 60deg = pi/3, 45deg = pi/4, 30deg = pi/6.

A chart is at:

https://en.wikipedia.org/wiki/File:Degree-Radian_Conversion.svg

12.5.2. Making plots of polynomials that approximate sin and cos

Let us first generate plots that approximate sin and cos for very small angles:

\[ \begin{align}\begin{aligned}\sin(x) \approx x\\\cos(x) \approx 1\end{aligned}\end{align} \]

Use your favorite plotting program to show the following. I give the examples for gnuplot and for desmos and geogebra:

$ gnuplot
# then at the gnuplot> prompt:
set grid
plot [-1.5*pi:1.5*pi] [-1.5:1.5] sin(x)
replot x
replot cos(x)
replot 1

sin(x)
x
cos(x)
y = 1

Study this and make a guess as to where x is a good approximation to sin(x), and where 1 is a good approximation to cos(x). Set your calculator to radians and calculate how far off the approximation is for those values of x you come up with.

The next terms in the sin and cos series are:

\[ \begin{align}\begin{aligned}\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \frac{x^{11}}{11!} \dots\\\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \frac{x^{10}}{10!} \dots\end{aligned}\end{align} \]

Continue approximating the plots for sin and cos with higher degree polynomials, for example with the instructions below, and every time make an estimate (and then calculate it) for where they start diverging.

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
set grid
plot [-6:6] [-1.5:1.5] sin(x) lw 3
replot x
replot x - x**3 / 3!
replot x - x**3 / 3! + x**5 / 5!
replot x - x**3 / 3! + x**5 / 5! - x**7 / 7!
replot x - x**3 / 3! + x**5 / 5! - x**7 / 7! + x**9 / 9!

sin x
x
x - x^3 / 3!
x - x^3 / 3! + x^5 / 5!
x - x^3 / 3! + x^5 / 5! - x^7 / 7!
x - x^3 / 3! + x^5 / 5! - x^7 / 7! + x^9 / 9!

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
set grid
plot [-6:6] [-1.5:1.5] cos(x) lw 3
replot 1
replot 1 - x**2 / 2!
replot 1 - x**2 / 2! + x**4 / 4!
replot 1 - x**2 / 2! + x**4 / 4! - x**6 / 6!
replot 1 - x**2 / 2! + x**4 / 4! - x**6 / 6! + x**8 / 8!
replot 1 - x**2 / 2! + x**4 / 4! - x**6 / 6! + x**8 / 8! - x**10 / 10!

(cos x)
1
1 - x^2 / 2!
1 - x^2 / 2! + x^4 / 4!
1 - x^2 / 2! + x^4 / 4! - x^6 / 6!
1 - x^2 / 2! + x^4 / 4! - x^6 / 6! + x^8 / 8!
1 - x^2 / 2! + x^4 / 4! - x^6 / 6! + x^8 / 8! - x^10 / 10!

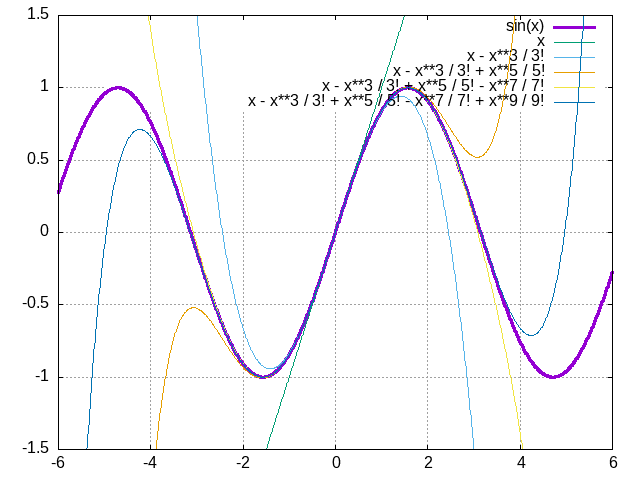
Figure 12.5.1 The first few polynomial approximations for the sin functions. The thicker line is the sin function, and the thinner ones are the ever-improving polynomial approximations.

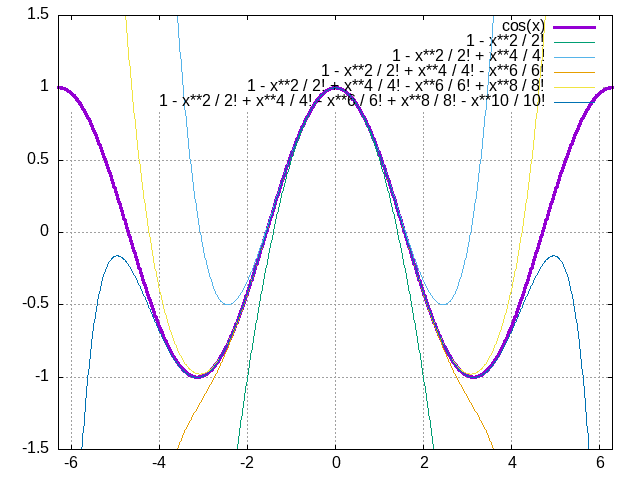
Figure 12.5.2 The first few polynomial approximations for the cos functions. The thicker line is the cos function, and the thinner ones are the ever-improving polynomial approximations.

What is the take-home from these two figures? What they show us is that you can approximate \(sin(x) \approx x\) for small values of \(x\). You can also approximate \(cos(x) \approx 1 - x^2/2!\) for small values of \(x\).

12.6. Starting to study exponentials

12.6.1. Plotting some exponentials

We first get used to exponentials by looking at \(10^x\) and comparing it to polynomial growth. In gnuplot:

$ gnuplot
# then at the gnuplot prompt:
reset
set grid
set xrange [0:4]
plot 10**x
replot x
replot x**2
replot x**3
replot x**4
replot x**5
replot x**6
replot x**7

And in desmos/geogebra:

10^x
x
x^2
x^3
x^4
x^5
x^6
x^7

Aha! \(x^7\) grew faster than \(10^x\) in the region from 0 to 4. But wait: we have been told that exponential functions will always outpace polynomials eventually. So how do we resolve that?

Experiment: how far out do you have to go in x before \(10^x > x^7\)? How would you explore that?

(Here we pause while everyone tries it out on their own notepad, and then we compare what we came up with.)

Now let us explore smaller bases for the exponential function:

$ gnuplot
# in gnuplot:
reset
set grid
set xrange [-4:4]
plot 10**x
replot 2**x
# 2**x was tiny!  how does it compare to polynomials?
plot 2**x
replot x**2
# zoom in closer:
set xrange [0:5]
plot 2**x
replot x**2

10^x
2^x
x^2

With a lot of zooming in, this shows that \(2^x\) eventually outgrows \(x^2\). Exercise: explore how long it takes for \(2^x\) to outgrow \(x^7\)?

And with very very small bases:

$ gnuplot
# in gnuplot:
set xrange [0:20]
plot 1.1**x
plot x**7

1.1^x
x^7

show how long it takes for \(1.1^x\) to outgrow \(x^7\).

12.6.2. The number \(e\): base for natural exponentials and logarithms

Now let us start looking at base \(e\) and why it is such a special number. We will mostly shift to working out of the OpenSTAX Algebra and Trigonometry book, the chapter on exponential and logarithmic functions. But we will mention here that \(\exp(x) = e^x\) uses a special number \(e\) as a base, and we experiment with calculating \(e\) like this:

\[e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} + \dots = \sum_{k=0}^{\infty} \frac{1}{k!} \approx 2.71828182846\]

But we take a break from these notes as we get to use a proper text book to explore exponentials and logarithms in more detail.

12.6.3. The Taylor series for \(e^x\)

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
reset
set grid
set xrange [-1:3]
set terminal qt linewidth 3
plot exp(x) lw 2
replot 1
replot 1 + x
replot 1 + x + x**2 / 2!
replot 1 + x + x**2 / 2! + x**3 / 3!
replot 1 + x + x**2 / 2! + x**3 / 3! + x**4 / 4!
replot 1 + x + x**2 / 2! + x**3 / 3! + x**4 / 4! + x**5 / 5!
replot 1 + x + x**2 / 2! + x**3 / 3! + x**4 / 4! + x**5 / 5! + x**6 / 6!

Discuss what you see here, then expand the x range and plot again:

# then try to expand the x range and replot
set xrange [-1:8]
replot

12.7. Miscellaneous Taylor expansions

Logarithms:

\[\begin{split}log(1 - x) = -\sum_{k=1}^{\infty} \frac{x^k}{k} \\ log(1 + x) = \sum_{k=1}^{\infty} (-1)^{k+1} \frac{x^k}{k}\end{split}\]

the first when \(|x| < 1\), the second when \(-1 < x \leq 1\)

Note that when you plot these logarithmic functions you will need to double check that your plotting program uses \(log()\) for natural logarithms. Some of the use \(\ln()\)

Geometric series:

\[\begin{split}\frac{1}{1-x} & = & \sum_{k=0}^{\infty} & x^k \\ \frac{1}{(1-x)^2} & = & \sum_{k=1}^{\infty} & k x^{k-1} \\ \frac{1}{(1-x)^3} & = & \sum_{k=2}^{\infty} & \frac{(k-1)k}{2} x^{k-2}\end{split}\]

when \(|x| < 1\)

12.8. Some square root expansions

Square root functions can get complicated. For example, the relativistic formula for the rest plus kinetic energy of an object with mass \(m_0\) is

\[E_{\rm total} = \frac{m_0 c^2}{\sqrt{1 - \frac{v^2}{c^2}}}\]

This has the famous Lorenz gamma factor:

\[\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]

We sometimes use a shorthand \(\beta = v/c\), where \(\beta\) is the velocity expressed as a fraction of the speed of light, and get:

\[\gamma = \frac{1}{\sqrt{1 - \beta^2}}\]

The first few terms in the taylor series expansion in \(\beta\) are (see the Cupcake Physics link in the resources chapter for details):

\[\begin{split}\gamma & = \; & 1 & + \frac{1}{2}\beta^2 + \frac{3}{8}\beta^4 + \frac{5}{16}\beta^6 + \dots\\ & = \; & 1 & + \frac{1}{2}\frac{v^2}{c^2} + \frac{3}{8}\frac{v^4}{c^4} + \frac{5}{16}\frac{v^6}{c^6} + \dots\end{split}\]

Putting this back into the formula for energy we get:

\[\begin{split}E_{\rm kinetic} & = \; & \frac{m_0 c^2}{\sqrt{1 - \frac{v^2}{c^2}}} \\ & = \; & m_0 c^2 + \frac{1}{2} m_0 v^2 + \dots\end{split}\]

For low values of \(v^2/c^2\) (i.e. \(v\) much slower than the speed of light) we have:

\[E_{\rm total} = m_0 c^2 + \frac{1}{2} m_0 v^2 + \dots\]

We can read off the terms and realize that the total energy is equal to the famous rest mass \(E_{\rm rest} = m_0 c^2\) plus the kinetic energy \(\frac{1}{2} m_0 v^2 + \dots\):

\[E_{\rm total} = E_{\rm rest} + E_{\rm kinetic} = m_0 c^2 + \frac{1}{2} m_0 v^2 + \frac{3}{8} m_0 \frac{v^4}{c^2} \dots\]

Let us explore the Lorenz gamma factor for values of \(v\) in the whole range from 0 to \(c\):

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
reset
set grid
set ylabel '\gamma'
set xlabel '\beta (v^2/c^2)'
set xrange [0:1]
set terminal qt linewidth 3
plot 1 / (1 - x**2)

Figure 12.8.1 The lorenz factor as a function of \(\beta = v^2/c^2\). Note how it is close to 1 for most of the run, but grows out of control when \(v\) approaches the speed of light \(c\).

What insight does this give us on the energy of an object as it approaches the speed of light? Note that the formulae for length and time are:

\[\begin{split}L = \frac{1}{\gamma} L_0 \\ \Delta t' = \gamma \Delta t\end{split}\]

so the behavior of \(\gamma\) as a function of \(\beta\) (and thus \(v\)) also affects length and time.

Now let us look at the polynomial approximates in \(\beta\):

$ gnuplot
## then the following lines have the prompt gnuplot> and we type:
reset
set grid
set ylabel '\gamma'
set xlabel '\beta (v^2/c^2)'
set xrange [0:0.0001]
set terminal qt linewidth 3
plot 1 / (1 - x**2)
replot 1
replot 1 + (1.0/2) * x**2
replot 1 + (1.0/2) * x**2 + (3.0/8) * x**4
replot 1 + (1.0/2) * x**2 + (3.0/8) * x**4 + (5.0/16) * x**6

12.9. The pendulum: the equation and how to simplify it

The “simple pendulum” is a classic physics setup shown in Figure 12.9.1.

Figure 12.9.1 A force diagram of a simple pendulum. Because of the constraint of the string, the force of gravity acting on the mass in the direction of montion is \(mg \sin(\theta)\)

(Figure credit: wikipedia https://commons.wikimedia.org/wiki/File:Pendulum_gravity.svg licenced under the CC BY-SA 3.0 license.)

Here is how to think about these diagrams: the quantity \(\theta\) is a function of time – we could write it fully as \(\theta(t)\), since it will change with time as the pendulum swings.

Our scientific question then becomes: can you “solve” this equation, writing an expression:

\[\theta(t) = {\rm SomeFunctionExpression(t)}\]

The terminology used in physics is that we need to “solve Newton’s second equation” to find \(\theta.\)

Looking at the force diagram in the picture, we see focus on a very short bit of the arc of the circle that the pendulum’s mass is constrained to travel. That arc leads from the current position.

From geometry we know that the length of a bit of arc is:

\[\Delta {\rm ArcLength} = l \Delta(\theta)\]

where l is the length of the string. That expression \(l\theta\) is what will be used as a displacement in the classical physics equations.

Some simple trigonometry will tell us that for this system Newton’s 2nd law (\(F = m \frac{d^2(l \theta)}{dt^2}\)), combined with the force of gravity for a falling body (\(F_{\rm gravity} = -mg\sin(\theta)\)) will give us (after we simplify for \(m\) which appears on both sides):

\[\begin{split}l \frac{d^2\theta}{dt^2} = -g\sin(\theta) \\ \frac{d^2\theta}{dt^2} + \frac{g}{l} \sin(\theta) = 0\end{split}\]

We use the name \(\omega_0\) (angular frequency) to refer to \(\sqrt{l/g}\), and we get:

\[\frac{d^2\theta}{dt^2} + \omega_0^2 \sin(\theta) = 0\]

At this time we are not yet looking at differential equations in detail, so we will simply mention (for those who have already studied them) that the general solution to this is very very difficult to find: it involves some advanced and subtle mathematical techniques, and the calculation of what are called elliptical integrals.

For a discussion of the general solution you can follow this video:

https://www.youtube.com/watch?v=efvT2iUSjaA

But the important thing to say here is that if \(\theta\) is a small angle, then we can approximate it with: \(\sin(\theta) \approx \theta\) and our equation becomes:

\[\begin{split}\frac{d^2\theta}{dt^2} + \omega_0^2 \theta = 0 \\ {\rm or} \\ \frac{d^2\theta}{dt^2} = - \omega_0^2 \theta\end{split}\]

Now we can do some experiments to say: “hey, if you have a function where the slope of the slope of that function is equal to minus the function itself, what does that look like?

We will save the full study of differential equation (even this simpler one) for later on in the working group, but we will give ourselves an idea with some plots.

First of all: let us look at the plot of an exponential function. How does the slope of that plot change as we move out on the function?

Then let us plot the \(\sin(x)\) and \(\cos(x)\) functions one above the other. we will notice that the slope of one looks a lot like the other one.

And the slope of the other one looks a lot like the first one, but negative.

And our mind that loves to make connections will notice that: “the slope of the slope of \(\sin(x)\) is…!”

12.10. Taylor series, and an intuition on why they work

12.10.1. Nomenclature

Remember: we always want to demistify terminology, so let’s see what names mathematicians use to talk about these series we have experimented with.

The kinds of series we work with most of the time are called power series. They have the form:

\[\sum_{k=0}^{N} c_k x^k\]

where \(c_k\) are constant coefficients. The name “power series” comes from the fact we have increasing powers of \(x\).

There is a particular type of power series called the Taylor series. The Taylor series is a wonderful tool which allows you to approximate a function near a certain point, let’s call it \(a\). It looks like:

(12.10.1)\[S(x) = \sum_{k=1}^{\infty} \frac{f^{(k)}(a)}{k!} (x - a)^k\]

This formula is dense, so let’s unpack the two parts of it.

There are the coefficients, which are constants (they do not depend on \(x\)): \(\frac{f^{(k)}(a)}{k!}\).

And there is the power term \((x-a)^k\), which does depend on \(x\).

So this looks like a polynomial of very high degree (you could almost say inifinite degree).

The series we saw above for \(sin(x)\), \(cos(x)\), and \(e^x\) are all examples of Taylor series. They are all centered at zero, and the coefficients are the derivatives of the function, evaluated at zero. In class we can work out what all those derivatives are, and check that the formula we have been using is indeed the Taylor series.

You can understand this formula at two levels: you can either say “sure, when I made my plots I noticed that they approximate the sin, cos, and exponential functions nicely.”

Or you can say “hey that’s really cool: I wonder how those high order derivatives come in to it”.

12.10.2. Intuition on the Taylor Series derivatives

This is a good topic to develop with the first class. By looking at Figure 12.5.1 we can see how the various higher derivatives in the sin function in Equation (12.10.1) nudge our series to get closer and closer to the actual value of the function.

[This writeup will continue when the working group has come up with a good way of describing that intuition.]

12.11. A historical diversion: Bhaskara I’s formula

https://en.wikipedia.org/wiki/Bhaskara_I%27s_sine_approximation_formula