14. Fourier analysis on real data

In the previous chapter we learned about Fourier Analysis and showed how to take the Fourier transform of some known functions.

Here we will show how to apply the Fourier transform to “data”, for example to data coming from experiments. We will start with some artificial data, and then look at the output from an experiment.

14.1. What’s hidden in noisy data?

Fourier analysis suggests that we could think of the spectrum (how strong each frequency is in a signal) as a sort of “character” of the signal: a deep description which might not be obvious on the surface, but it is there.

Here we will do some experiments to demonstrate this idea, and then we will use this idea to devise a marvel of data analysis: signal filtering.

14.1.1. A contrived double-period signal

Start with this plot:

$ gnuplot
# at the gnuplot> prompt type:
set samples 1000
plot sin(x) + 0.3*sin(365*x)

Then we will download the program code/filter_toy.py and look at how it works. Then we will run it with:

python3 filter_toy.py

to see an output like that in Figure 14.1.1.

Figure 14.1.1 An example of filtering for a very simple signal: the sum of 3 sin waves. The first filter zeros out all the high frequency fourier coefficients (low pass filter). The second one zeroes out all the low frequency fourier coefficients (high pass filter).

14.1.2. An artificial noisy signal

Now we will download the program code/filter_random.py and look at how it works. Then we will run it with:

python3 filter_random.py

to see an output like that in Figure 14.1.2.

Figure 14.1.2 An example of filtering for a noisy signal: a sin() wave with random noise added to it. The first filter zeros out all the high frequency fourier coefficients (low pass filter). The second one zeroes out all the low frequency fourier coefficients (high pass filter).

The instructor can now experiment changing the 0.4*np.random.randn(...) to be 3.4* – this will dwarf the signal with noise, but we will still find an approximate sin wave.

Another interest change is to apply the lowpass filter to the highpass filter result (instead of to the original signal). This will give a bandpass filter: a narrow band around the fundamental frequency.

All these experiments can be done live in class.

14.1.3. Experimental double-period noisy data

Let us explore the data from a weather station. We will pick the Las Cruces weather station from the climate research network coordinated by NOAA (National Oceanic and Atmospheric Administration).

We will find that this data has both the features we saw above: it has an underlying doubly periodic behavior, and it also has noise. It also has plenty more information, related to weather (and, over the course of many years) climate change, but we will focus on finding the two periodic signals, and on the noise.

Start with:

wget https://www.ncei.noaa.gov/pub/data/uscrn/products/subhourly01/2014/CRNS0101-05-2014-NM_Las_Cruces_20_N.txt

Then plot the 9th column in gnuplot with:

$ gnuplot
# then at the gnuplot> promt type:
plot 'CRNS0101-05-2014-NM_Las_Cruces_20_N.txt' using 9 with lines

We immediately see two undesirable spikes that come down to almost -10000. We spend some time looking at the file, we puzzle over it, and then realize that:

Caution

Data often needs cleaning. In this case you see that an old (and poor) programmer habit crept into the pipeline of programs that generated this data: when samples were missing they replaced them with -9999.0.

The files are also a jumble of numbers, so to understand what is in those files we visit https://www.ncei.noaa.gov/pub/data/uscrn/products/subhourly01/headers.txt and https://www.ncei.noaa.gov/pub/data/uscrn/products/subhourly01/readme.txt to see what columns mean what.

We conclude that we have data spaced out by 5 minutes, and the 9th column is a temperature reading, and that we need to eliminate all lines that have -9999.0 in them:

grep -v -e -9999.0 CRNS0101-05-2014-NM_Las_Cruces_20_N.txt > Las_Cruces_filtered.txt
$ gnuplot
# then at the gnuplot> prompt type:
plot 'Las_Cruces_filtered.txt' using 9 with lines

We might want to look at more than one year of data. We can do this with:

for year in 2014 2015 2016
do
    wget https://www.ncei.noaa.gov/pub/data/uscrn/products/subhourly01/${year}/CRNS0101-05-${year}-NM_Las_Cruces_20_N.txt
done
cat CRNS*Las_Cruces*.txt | grep -v -e -9999.0 > temperatures.dat

and now we have several years to plot:

$ gnuplot
# then at the gnuplot> prompt type:
plot 'temperatures.dat' using 9 with lines

Now let us download the program code/temperature_fft.py that analyzes this data with the fourier transform, and run it:

python3 temperature_fft.py

Caution

These are big data files: 5 minute intervals for a year make for more than 100 thousand samples per year. Three years of data will require the Fourier transform of a signal with more than 300000 samples, which might strain the CPU and/or memory of your computer. This might be even more of a problem if you use an web-based python interpreter.

14.2. A breather and some terminology

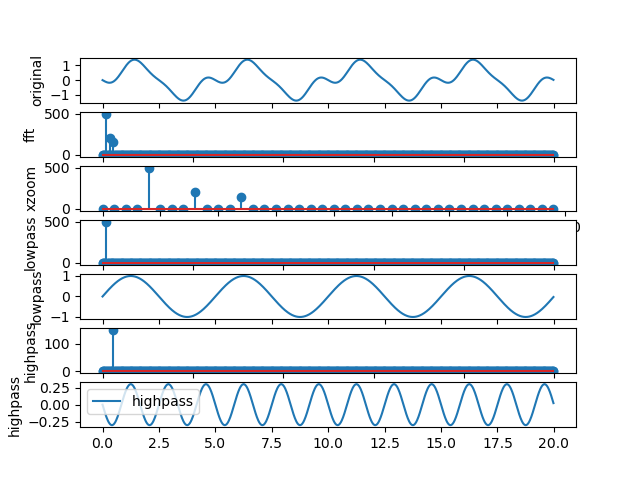
We have just gone through three examples of using the Fourier transform on real data. This was a lot of new material, so let us take a moment and discuss what we have seen.

First some terminology that accompanies these new ideas:

Continuous Fourier Transform

The coefficients of the sin and cos functions at various frequencies which allow us to reproduce a periodic function of continuous time. We discussed this in Section 13

Discrete Fourier Transform (DFT)

A form of Fourier analysis that is applicable to a sequence of values. Instead of a function \(f(t)\) with \(t\) being a real number, we have a function given by pairs \({t_k, f_k}\). The \(t_k\) values are discrete time samples, and \(f_k\) are the samples of the function at those time points. The DFT is clearly what we will be using to examine experimental data.

Fast Fourier Transform (FFT)

An algorithm to calculate the DFT in \(O(N\log N)\) time instead of \(O(N^2)\). This is also known as the Cooley Tuckey algorithm.

So is it DFT or FFT?

The FFT is used almost universally to calculate the DFT, so FFT is sometimes used to mean the specific algorithm used, and sometimes just as a placeholder for DFT.

Signal processing

A field of electrical engineering focused on analyzing, modifying, and synthesizing signals. Signals can refer to sound, images, and scientific measurements.

Noise

Unwanted distortions that a signal can suffer during propagation, transmission, and processing. Often the specific origin of the noise cannot be picked out, but it can be modeled in various ways that help with finding a signal that might otherwise be obscured.

White noise

A form of noise that gets added to a signal and that has equal intensity at different frequencies. In acoustics it sounds like a hissing sound.

14.3. Fourier analysis: sound and music

When we mentioned waves with different frequencies you might have thought of sound, and you would have been right. Fourier analysis is a good tool for understanding what makes up sound waves.

Let us take a tour through a series of signals, and we will look at their fourier transforms.

14.3.1. Tuning fork

A tuning fork puts out a very pure single \(\sin\) wave at a “middle A” note, also known as \(A_4\) or concert pitch. \(A_4\) has a frequency of 440 Hz.

We can download a stock mp3 file of the sound of a tuning fork, then we can use standard command line utilities to convert it to a text file. For example:

wget https://freesound.org/data/previews/126/126352_2219070-lq.mp3 -O tuning-fork.mp3
# convert through various steps to .aif and then to .dat
ffmpeg -i tuning-fork.mp3 tuning-fork.aif
sox tuning-fork.aif tuning-fork.dat
ls -lsh tuning-fork.*
# check out what it sounds like with
vlc tuning-fork.mp3

You can plot it with:

gnuplot
# then at the gnuplot> prompt:
plot 'tuning-fork.dat' using 1:2 with lines

This shows you the plot of amplitude versus time, and you should notice some correspondence between it and the sound you heard - the person who recorded this file kept modulating how loud it was.

But that does not tell us what frequencies are in it! Let us adapt the filter_random.py program to work with this data file.

You can download code/fft_audio.py and try running it on this tuning-fork.dat file:

python3 fft_audio.py

So the bottom line is: once we have it as a text file we can do the following:

• Use our standard plotting techniques to see that it looks like a \(\sin\) wave, but with lots of amplitude variation.

• Write a program which uses the powerful Python scientific libraries to calculate the Fourier transform of the tuning fork signal.

• Look at the Fourier transform, hoping to see that a clean \(\sin\) wave will appear as a single spike, indicating that there is only one \(\sin\) wave in the signal.

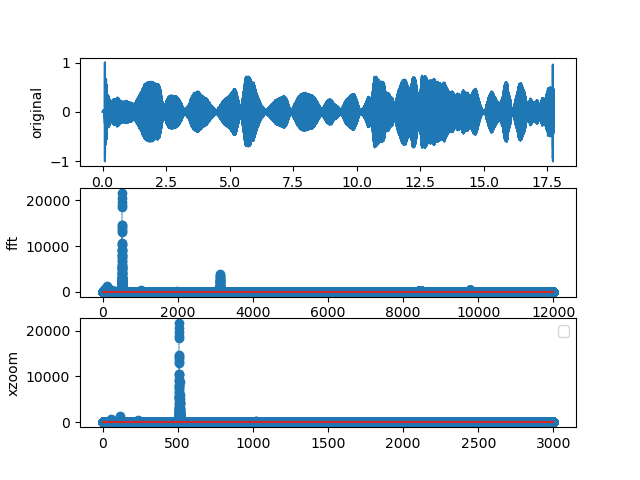
Figure 14.3.1 The FFT of a tuning fork. Notice the single dominant frequency, which shows that the tuning fork is close to being a perfect \(\sin()\) wave.

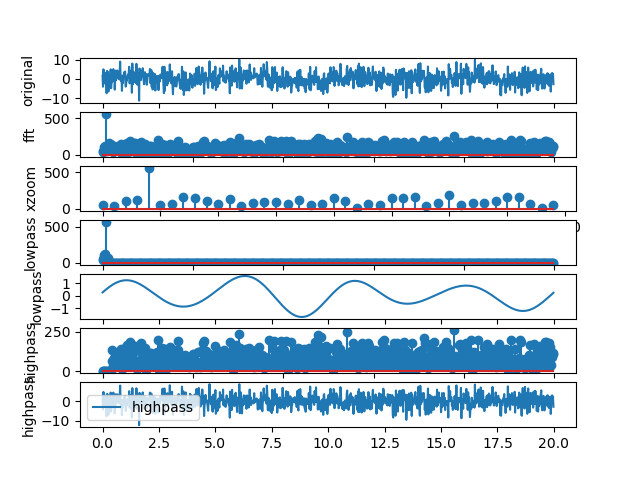
14.3.2. White noise

Now let us download an example of white noise. This is a random wave with no discernible pattern.

wget -q --continue http://www.vibrationdata.com/white1.mp3 -O white-noise.mp3
ffmpeg -n -i white-noise.mp3 white-noise.aiff
sox -q white-noise.aiff -t dat white-noise.dat
head -7000 white-noise.dat | tail -2000 > white-noise-small-sample.dat
# check out what it sounds like with
vlc white-noise.mp3

Notice how we removed some data from the start and some from the end so as to have a shorter data file.

gnuplot
# then at the gnuplot> prompt:
reset
set grid
plot 'white-noise-small-sample.dat' with lines

Now change fft_audio.py to have fname = white-noise-small-sample.dat and run it again.

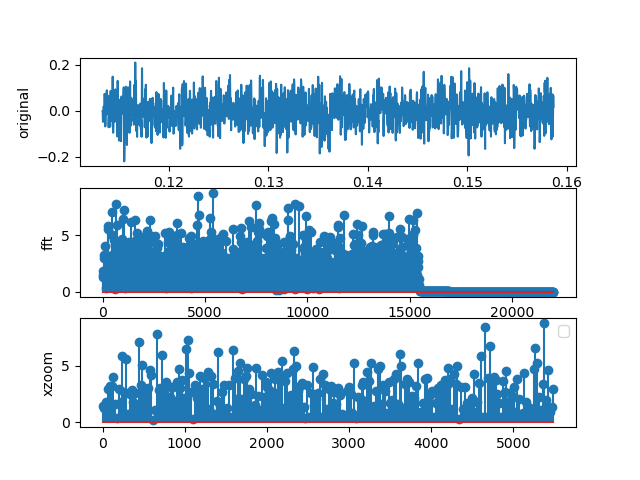
Figure 14.3.2 The FFT of a white noise sample. Notice the broad and flat value of the transform for almost all the frequencies.

You could say that the Fourier spectrum for white noise is the opposite of that for the pure tuning fork signal: instead of a single spike you have random-looking spikes all over the spectrum.

14.3.3. Violin playing single “F” note

Now let us look at some musical notes from real instruments. Each note corresponds to a certain frequency [Backus, 1977]. shows a much more complex signal than the tuning fork.

wget --continue http://freesound.org/data/previews/153/153595_2626346-lq.mp3 -O violin-F.mp3
ffmpeg -n -i violin-F.mp3 violin-F.aiff
sox violin-F.aiff -t dat violin-F.dat
python3 fft_audio.py violin-F.dat

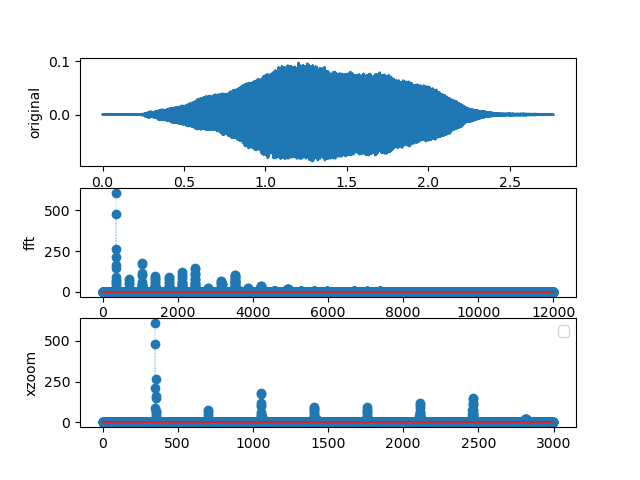
Figure 14.3.3 The FFT of a violin play an F note.

The signal in has some structure to it. The Fourier transform has several peaks: the strongest peak (for a \(A_4\) note) will be at the fundamental frequency of 440 Hz, but there are many other peaks. The pattern of the peaks characterizes the sound of that specific violin (or guitar or other instrument).

14.3.4. Violin playing single “A” note

This is a repeat of but with a different note on the violin: F instead of A. is hard to distinguish from since the character of the instrument is the same. At this point we have not written code to plot the actual frequencies on the \(x\) axis, so we cannot spot that the \(A_4\) note has its highest peak at 440Hz, while the \(F_5\) is at 698.45Hz [Backus, 1977].

wget --continue http://freesound.org/data/previews/153/153587_2626346-lq.mp3 -O violin-A-440.mp3
ffmpeg -n -i violin-A-440.mp3 violin-A-440.aiff
sox violin-A-440.aiff -t dat violin-A-440.dat
python3 fft_audio.py violin-A-440.dat

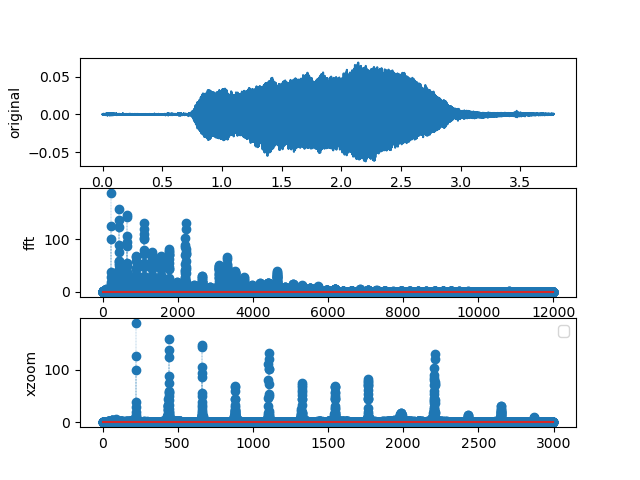
Figure 14.3.4 The FFT of a violin play a middle A note.

14.3.5. A more complex music clip

The Pachelbel Canon is a well-known piece of baroque classical music which starts with a single note that is held for a while. shows the signal and its Fourier transform, where you can identify a dominant peak.

wget -q --continue http://he3.magnatune.com/music/Voices%20of%20Music/Concerto%20Barocco/21-Pachelbel%20Canon%20In%20D%20Major%20-%20Johann%20Pachelbel%20-%20Canon%20And%20Gigue%20For%20Three%20Violins%20And%20Basso%20Continuo%20In%20D%20Major-Voices%20of%20Music_spoken.mp3 -O Canon.mp3
ffmpeg -n -i 'Canon.mp3' Canon.aiff
sox -q Canon.aiff -t dat Canon.dat
head -50000 Canon.dat | tail -4000 > canon-small-sample.dat
python3 fft_audio.py canon-small-sample.dat

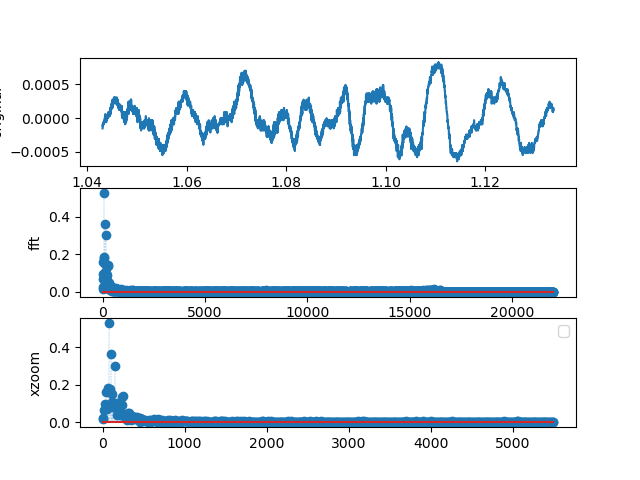
Figure 14.3.5 The FFT of the first few seconds of the Pachelbel canon.

But what happens if we have music that is not a single note? In we will look at a clip of a choir singing Gloria in Excelsis Deo. The clip (which you can play with vlc gloria.ogg after downloading it) starts in a place where many voices are singing in harmony, so there is no single note to be picked out.

wget -q --continue https://upload.wikimedia.org/wikipedia/en/e/ea/Angels_We_Have_Heard_on_High%2C_sung_by_the_Mormon_Tabernacle_Choir.ogg -O gloria.ogg
ffmpeg -n -i gloria.ogg gloria.aiff
sox -q gloria.aiff -t dat gloria.dat
python3 fft_audio.py gloria.dat

We expect to see several different peaks in the Fourier spectrum, and that is what you see in the second panel of this plot.

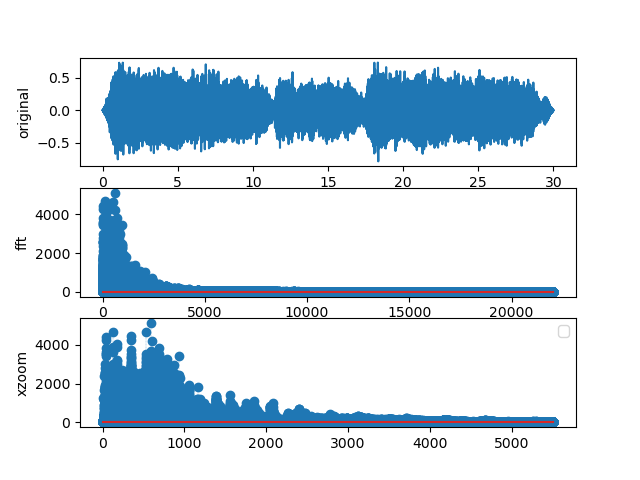
Figure 14.3.6 The FFT of the first few seconds of Gloria in Excelsis Deo.

14.3.6. Create your own audio clip and analyze it

Record some sound and analyze it.

The program sox, which we used to do audio format conversion, comes with two other programs rec (to record from your computer’s microphone) and play to play those files back.

To try it out I ran the following:

rec mark-guitar-sample.dat
## I played a few guitar notes near the laptop microphone,
## emphasizing low and high frequences, then I hit control-C
play mark-guitar-sample.dat
python3 fft_audio.py mark-guitar-sample.dat

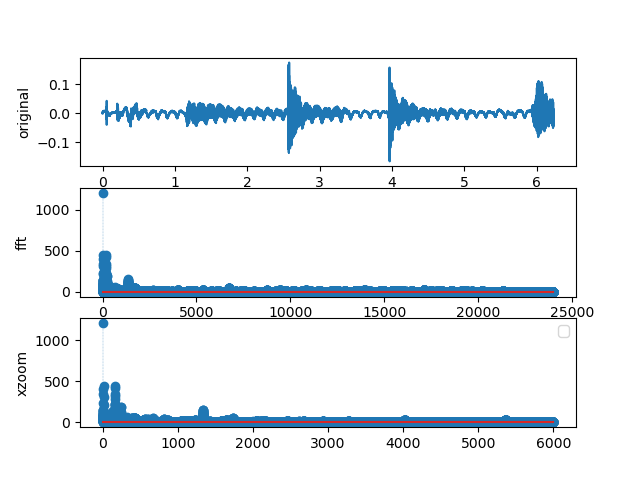
Figure 14.3.7 The FFT of my own musical sample.

Now try doing this again for different things you can record with your microphone. If you have a tuning fork, tap it and then rest it on a guitar’s soundboard and record that, see if you get something similar to what we saw when we discussed tuning forks. If you have a musical instrument, try recording an A note or an F note and compare them to what we discussed violins.